CEL18702 2016 2 AULA09: mudanças entre as edições
Página substituída por 'teste' |
Sem resumo de edição |
||
| Linha 1: | Linha 1: | ||
=Circuitos Equivalentes= | |||
Qualquer circuito linear (fontes independentes) pode ser substituído, em dois terminais A e B, por uma fonte de tensão em série <math>V_{Th}\,</math> com uma resistência <math>R_{Th}\,</math>, sendo que: | |||
:A tensão <math>V_{Th}\,</math> é o valor da diferença de potencial entre os terminais A e B, quando a rede linear do resto do circuito (diferença de potencial entre A e B em circuito aberto) é isolado. | |||
:A resistência <math>R_{Th}\,</math> é a resistência vista a partir dos terminais A e B, e é determinada por curto-circuito de todas as fontes de tensão e substituída por circuitos abertos em fontes de corrente. | |||
=Teoremas de circuitos= | |||
*Objetivo: Simplificar a análise de circuitos. | |||
*Aplicável: Somente a circuitos lineares. | |||
==Thevenin== | |||
O Teorema de Thévenin nos diz que podemos | |||
substituir todo o circuito, com exceção ao | |||
bipolo em questão, por um circuito equivalente | |||
contendo uma fonte de tensão em série com um | |||
resistor. | |||
[[Imagem:fig58_CEL18702.png|center]] | |||
<center> | |||
Figura 1 - Teorema de Thevenin. | |||
</center> | |||
==Norton== | |||
Por sua vez, o Teorema de Norton nos diz que | |||
podemos substituir todo o circuito, com | |||
exceção ao bipolo em questão, por circuito | |||
equivalente contendo uma fonte de corrente em | |||
paralelo com um resistor. | |||
[[Imagem:fig59_CEL18702.png|center]] | |||
<center> | |||
Figura 2 - Teorema de Norton. | |||
</center> | |||
=Logo= | |||
<math>R_{Th}=R_{Eq}\,</math> | |||
<math>V_{Th}=R_{Th}.I_N\,</math> | |||
<math>I_{N}=\frac{V_{Th}}{R_{Th}}\,</math> | |||
=Exemplo= | |||
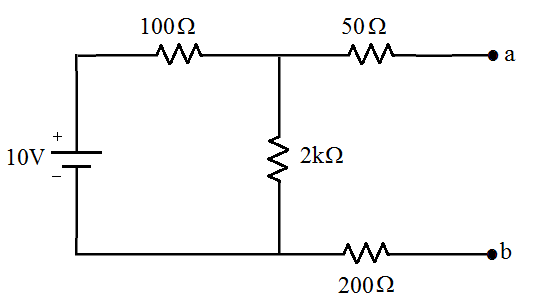
;[1] Calcule <math>V_{Th}\,</math>, <math>R_{Th}\,</math> e <math>I_{N}\,</math> para o circuito abaixo: | |||
[[Imagem:fig39_CEL18702.png|center]] | |||
;Resultado: | |||
{{collapse top|Solução}} | |||
Lembrando: | |||
Para tornar o circuito mais simples: | |||
#Calcular tensão de circuito aberto; | |||
#Calcular corrente de curto circuito; | |||
#Obter <math>R_{Th}\,</math>, <math>V_{Th}\,</math> ou <math>I_N\,</math>. | |||
;Parte [1] | |||
[[Imagem:fig39a_CEL18702.png|center]] | |||
<math>V_{ab}=\frac{10.2000}{2000+100}=9,5V\,</math> | |||
<math>V_{ab}=V_{Th}\,</math> | |||
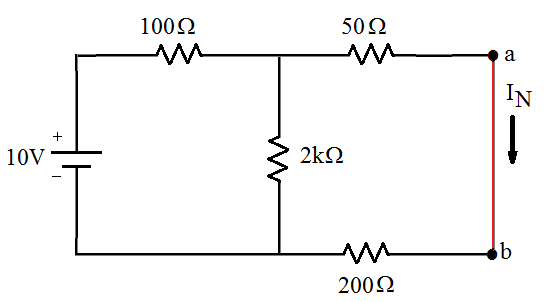
[[Imagem:fig39b_CEL18702.png|center]] | |||
;Parte [2] | |||
<math>R_{eq}= 2k // (50+200)=222,2\, \Omega</math> | |||
<math>V_{eq}=\frac{10.222,2}{100+222,2}=6,9V</math> | |||
<math>I_N=\frac{6,9}{50+200}=27,6mA</math> | |||
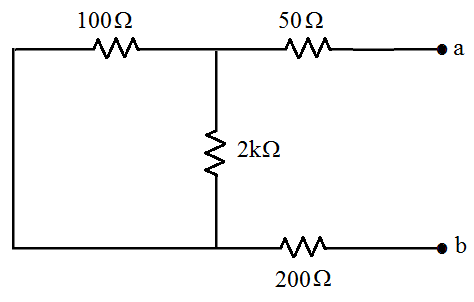
;Parte [3] | |||
- Cálculo de <math>R_{Th}\,</math> matando as fontes: | |||
:Fontes de tensão em curto circuito; | |||
:Fontes de corrente em aberto; | |||
:Aplicar associação de resistores. | |||
<math>R_{Th}=\frac{V_{Th}}{I_N}=\frac{9,5}{27,6^{-3}}=344,2 \Omega\,</math> | |||
[[Imagem:fig39c_CEL18702.png|center]] | |||
<math>R_{eq}=50+(100//2000)+200=345,2\,\Omega</math> | |||
{{collapse bottom}} | |||
=Exercícios= | |||
[1] Calcule o circuito equivalente utilizando o teorema de Thevenin | |||
- Determine a tensão e a corrente na resistência de carga de 70k<math>\Omega</math>. | |||
[[Imagem:fig40_CEL18702.png|center]] | |||
- Lembre-se: Você deve fazer os cálculos sem o o resistor de 70k<math>\Omega</math>. | |||
;Resultado: | |||
{{collapse top|Solução}} | |||
<math>V_{Th}=30V\,</math> | |||
<math>R_{Th}=35k\Omega\,</math> | |||
<math>I_{N}=0,854mA\,</math> | |||
Cálculo da resistência de Thevenin: | |||
<math>R_{Th}=(20.10^3//60.10^3)+(40.10^3//40.10^3)=35 k\Omega\,</math> | |||
Cálculo da tensão de Thevenin <math>V_{Th}=V_{AB}</math> | |||
<math>V_{Th}=V_{AB}=V_{40k}-V_{20k}</math> | |||
<math>V_{Th}=\frac{120.40.10^3}{40.10^3+40.10^3}-\frac{120.20.10^3}{20.10^3+60.10^3}=30V\,</math> | |||
Cálculo da resistência de Norton: | |||
<math>R_N=R_{Th}==35k\Omega\,</math> | |||
Cálculo da corrente de curto-circuito: | |||
<math>I_N=I_{20k}-I_{60k}\,</math> | |||
<math>R_{eq1}=(20.10^3//40.10^3)= 13,3k\Omega\,</math> | |||
<math>R_{eq2}=(60.10^3//40.10^3)= 24k\Omega\,</math> | |||
<math>V_1=\frac{120.24.10^3}{24.10^3+13,3.10^3}=77,2V\,</math> | |||
<math>I_{20k}=\frac{120-77,2}{20.10^3}= 2,14mA\,</math> | |||
<math>I_{60k}=\frac{77,2}{60.10^3}= 1,29mA\,</math> | |||
<math>I_N=2,14.10^{-3}-1,29.10^{-3}=0,854mA\,</math> | |||
{{collapse bottom}} | |||
[2] Determinar a corrente no resistor <math>R_{AB}</math> utilizando o teorema de Thevenin. | |||
[[Imagem:fig41_CEL18702.png|center]] | |||
- Lembre-se: Você deve fazer os cálculos sem o o resistor de 10<math>\Omega</math>. | |||
;Resultado: | |||
{{collapse top|Solução}} | |||
<math>V_{Th}=-14V\,</math> | |||
<math>R_{Th}=6,6\Omega\,</math> | |||
{{collapse bottom}} | |||
[3] Diga qual o valor da resistência que solicita uma corrente de 5A quando ligada aos pontos a e b do circuito abaixo: | |||
[[Imagem:fig42_CEL18702.png|center]] | |||
{{collapse top|Solução}} | |||
<math>R=6\Omega\,</math> | |||
{{collapse bottom}} | |||
[4] Encontre o equivalente de Norton para o circuito abaixo: | |||
[[Imagem:fig43_CEL18702.png|center]] | |||
{{collapse top|Solução}} | |||
<math>R_{Th}=16\Omega\,,V_{Th}=-50V</math> | |||
{{collapse bottom}} | |||
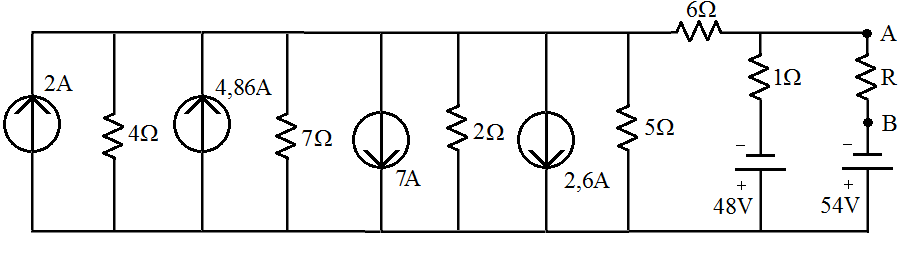
[5] Determine R para que a corrente que que passe pelos pontas A e B seja de 2A: | |||
[[Imagem:fig44_CEL18702.png|center]] | |||
{{collapse top|Solução}} | |||
[5.1] Substituindo as três primeiras fontes de tensão por fonte de corrente: | |||
[[Imagem:fig46_CEL18702.png|center|500px]] | |||
[5.2] Fazendo a substituição das quatro fontes de corrente em paralelo (teorema de Millman): | |||
<math>I_{eq}=2+4,86-7-2,6=-2,74A\,</math> | |||
[5.3] Fazendo a substituição da resistência equivalente desse paralelo: | |||
<math>\frac{1}{R_{eq}}=\frac{1}{4}+\frac{1}{7}+\frac{1}{2}+\frac{1}{5}=0,92\Omega\,</math> | |||
[5.4] Substituindo a fonte de corrente equivalente por fonte de tensão, juntamente com a resistência equivalente: | |||
<math>V_{eq}=I_{eq}.R_{eq}=-2,74*0,92=-2,52V\,</math> | |||
[[Imagem:fig46b_CEL18702.png|center|300px]] | |||
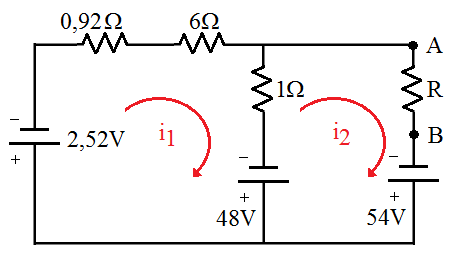
[5.5] Sabendo-se que a corrente <math>I_2=2A</math> tem-se: | |||
'''Malha 1''' | |||
<math>2,52+0,92i_1+6i_1+1(i_1-i_2)-48=0\,</math> | |||
<math>2,52+0,92i_1+6i_1+1i_1-2-48=0\,</math> | |||
<math>7,92i_1=48-2,52+2\,</math> | |||
<math>i_1=\frac{47,44}{7,92}=6 A\,</math> | |||
'''Malha 2''' | |||
<math>R.i_2-54+48+1(i_2-i_1)=0\,</math> | |||
<math>2R-54+48+1(2-6)=0\,</math> | |||
<math>R=\frac{54-48+4}{2}=5\Omega\,</math> | |||
;Resultado: | |||
<math>R=5\Omega\,</math> | |||
{{collapse bottom}} | |||
=Vídeo Aula= | |||
;Circuitos equivalentes Thevenin e Norton | |||
<center>{{#ev:youtube|389TqBn2LdM#!}} </center> | |||
=Referências= | |||
[1] http://www.decom.fee.unicamp.br/~cardieri/NotasdeAula_EA513/EA513_NotasAula_05.pdf | |||
[2] https://mesalva.com/ | |||
[3] http://moodle.planetfone.com.br/pluginfile.php/94/mod_resource/content/2/Teorema%20de%20thevenin%20e%20norton.pdf | |||
----- | |||
{| border="1" cellpadding="5" cellspacing="0" | |||
! style="background:#00BFFF;" | [[CEL18702_2016_2_AULA08 | << ]] | |||
! style="background:#778899;" | [[CEL18702_2016_2#Aulas | <> ]] | |||
! style="background:#00BFFF;" | [[CEL18702_2016_2_AULA10 | >> ]] | |||
|} | |||
Edição atual tal como às 13h11min de 11 de outubro de 2016
1 Circuitos Equivalentes
Qualquer circuito linear (fontes independentes) pode ser substituído, em dois terminais A e B, por uma fonte de tensão em série com uma resistência , sendo que:
- A tensão é o valor da diferença de potencial entre os terminais A e B, quando a rede linear do resto do circuito (diferença de potencial entre A e B em circuito aberto) é isolado.
- A resistência é a resistência vista a partir dos terminais A e B, e é determinada por curto-circuito de todas as fontes de tensão e substituída por circuitos abertos em fontes de corrente.
2 Teoremas de circuitos
- Objetivo: Simplificar a análise de circuitos.
- Aplicável: Somente a circuitos lineares.
2.1 Thevenin
O Teorema de Thévenin nos diz que podemos substituir todo o circuito, com exceção ao bipolo em questão, por um circuito equivalente contendo uma fonte de tensão em série com um resistor.
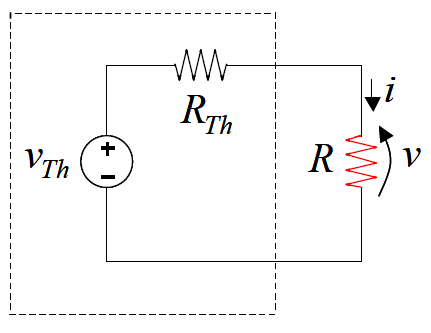
Figura 1 - Teorema de Thevenin.
2.2 Norton
Por sua vez, o Teorema de Norton nos diz que podemos substituir todo o circuito, com exceção ao bipolo em questão, por circuito equivalente contendo uma fonte de corrente em paralelo com um resistor.

Figura 2 - Teorema de Norton.
3 Logo
4 Exemplo
- [1] Calcule , e para o circuito abaixo
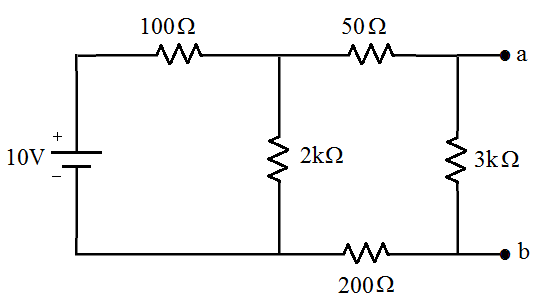
- Resultado
5 Exercícios
[1] Calcule o circuito equivalente utilizando o teorema de Thevenin
- Determine a tensão e a corrente na resistência de carga de 70k.
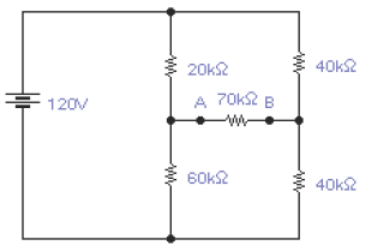
- Lembre-se: Você deve fazer os cálculos sem o o resistor de 70k.
- Resultado
| Solução |
|---|
|
Cálculo da resistência de Norton:
Cálculo da corrente de curto-circuito:
|
[2] Determinar a corrente no resistor utilizando o teorema de Thevenin.
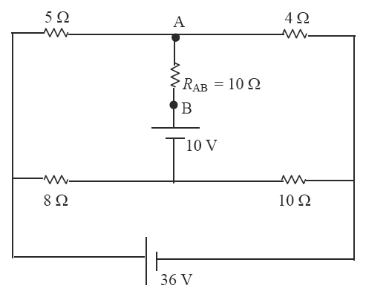
- Lembre-se: Você deve fazer os cálculos sem o o resistor de 10.
- Resultado
| Solução |
|---|
|
|
[3] Diga qual o valor da resistência que solicita uma corrente de 5A quando ligada aos pontos a e b do circuito abaixo:
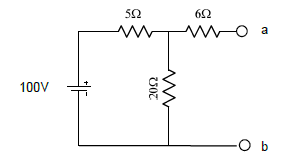
| Solução |
|---|
|
|
[4] Encontre o equivalente de Norton para o circuito abaixo:
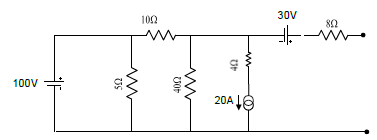
| Solução |
|---|
|
|
[5] Determine R para que a corrente que que passe pelos pontas A e B seja de 2A:
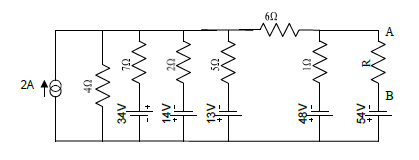
6 Vídeo Aula
- Circuitos equivalentes Thevenin e Norton
7 Referências
[1] http://www.decom.fee.unicamp.br/~cardieri/NotasdeAula_EA513/EA513_NotasAula_05.pdf
| << | <> | >> |
|---|