PRE-EngTel (Plano de Ensino): mudanças entre as edições
Ir para navegação
Ir para pesquisar
Sem resumo de edição |
Sem resumo de edição |
||
| (11 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 11: | Linha 11: | ||
:<SMALL>DISCIPLINAS SUCESSORAS: [[CSF-EngTel|CSF]], [[ADS-EngTel|ADS]], [[COM1-EngTel|COM1]] </SMALL><BR> | :<SMALL>DISCIPLINAS SUCESSORAS: [[CSF-EngTel|CSF]], [[ADS-EngTel|ADS]], [[COM1-EngTel|COM1]] </SMALL><BR> | ||
:<SMALL> MÓDULO PROFISSIONALIZANTE </SMALL><BR> | :<SMALL> MÓDULO PROFISSIONALIZANTE </SMALL><BR> | ||
;Ementa | |||
:Variáveis aleatórias. Definição e classificação de processo estocásticos. Processos contínuos e discretos no tempo. Classes de processos estocásticos. Processos Random Walk e Wiener. Processos de Poisson. Estacionariedade. Autocorrelação e representação espectral. Continuidade, Diferenciação e Integração. Ergodicidade e média no tempo. Decomposição espectral e expansão em séries. Resposta de sistemas lineares a entradas aleatórias. Processos Estocásticos especiais: processos autoregressivos, modelos “moving average”. Processos e sequências de Markov. Processos Gaussianos. Aplicação de processos estocásticos em Telecomunicações. | |||
;Objetivos | ;Objetivos | ||
*Conhecer os fundamentos da teoria da probabilidade, variáveis aleatórias e processos estocásticos. | |||
*Saber modelar e solucionar problemas de natureza probabilística, em particular aqueles com aplicações na área de telecomunicações. | |||
*Possuir conhecimento básico sobre a simulação em computador de experimentos probabilísticos. | |||
;Conteúdo Programático | |||
{{collapse top | bg=lightgreen | expand=true | Semestre 2016-1 - Prof. Roberto Nóbrega}} | |||
#Variáveis aleatórias (16h) | |||
##Funções massa, densidade e cumulativa | |||
##Variávels aleatórias mistas | |||
##Variáveis aleatórias conjuntamente distribuídas | |||
##Independência de variáveis aleatórias | |||
##Distribuição condicional | |||
#Valor esperado (8h) | |||
##Média, variância, momentos | |||
##Valor esperado de função de variável aleatória | |||
##Correlação e covariância | |||
##Valor esperado condicional | |||
#Vetores aleatórios (8h) | |||
##Vetor média e matriz covariância | |||
##Vetores aleatórios gaussianos | |||
#Definição e classificação de processos estocásticos (8h) | |||
##Processos contínuos e discretos | |||
##Especificação de processos estocásticos | |||
##Momentos de um processo estocástico | |||
##Estacionariedade e ergodicidade | |||
#Processos estocásticos estacionários no sentido amplo (8h) | |||
##Função autocorrelação | |||
##Densidade espectral de potência | |||
##Resposta de sistemas lineares a entradas aleatórias | |||
##Processos estocásticos gaussianos | |||
#Cadeias de Markov e processos de Poisson (6h) | |||
##Cadeias de Markov | |||
##Processos de Poisson | |||
##Introdução à teoria das filas | |||
{{collapse bottom}} | |||
{{collapse top | Semestre 2015-2 - Prof. Roberto Nóbrega}} | |||
#Variáveis aleatórias (12h) | |||
##Funções massa, densidade e cumulativa | |||
##Variáveis aleatórias mistas | |||
##Variáveis aleatórias conjuntamente distribuídas | |||
##Independência de variáveis aleatórias | |||
##Distribuição condicional | |||
#Valor esperado (12h) | |||
##Média, variância, momentos | |||
##Valor esperado de função de variável aleatória | |||
##Correlação e covariância | |||
##Valor esperado condicional | |||
#Vetores aleatórios (10h) | |||
##Vetor média e matriz covariância | |||
##Descorrelacionando variáveis aleatórias | |||
##Vetores aleatórios gaussianos | |||
#Definição e classificação de processos estocásticos (6h) | |||
##Processos contínuos e discretos | |||
##Especificação de processos estocásticos | |||
##Momentos de um processo estocástico | |||
##Estacionariedade e ergodicidade | |||
#Processos estocásticos estacionários no sentido amplo (8h) | |||
##Função autocorrelação | |||
##Densidade espectral de potência | |||
##Resposta de sistemas lineares a entradas aleatórias | |||
##Processos estocásticos gaussianos | |||
#Cadeias de Markov e processos de Poisson (6h) | |||
##Cadeias de Markov | |||
##Processos de Poisson | |||
##Introdução à teoria das filas | |||
{{collapse bottom}} | |||
{{collapse top | Semestre 2015-1 - Prof. Roberto Nóbrega}} | |||
#Variáveis aleatórias | |||
##Funções massa, densidade e cumulativa | |||
##Variávels aleatórias mistas | |||
##Variáveis aleatórias conjuntamente distribuídas | |||
##Independência de variáveis aleatórias | |||
##Distribuição condicional | |||
#Valor esperado | |||
##Média, variância, momentos | |||
##Valor esperado de função de variável aleatória | |||
##Correlação e covariância | |||
##Valor esperado condicional | |||
#Vetores aleatórios | |||
##Vetor média e matriz covariância | |||
##Descorrelacionando variáveis aleatórias | |||
##Vetores aleatórios gaussianos | |||
#Definição e classificação de processos estocásticos | |||
##Processos contínuos e discretos | |||
##Especificação de processos estocásticos | |||
##Momentos de um processo estocástico | |||
##Estacionariedade e ergodicidade | |||
#Processos estocásticos estacionários no sentido amplo | |||
##Função autocorrelação | |||
##Densidade espectral de potência | |||
##Resposta de sistemas lineares a entradas aleatórias | |||
##Processos estocásticos gaussianos | |||
#Cadeias de Markov e processos de Poisson | |||
##Cadeias de Markov | |||
##Processos de Poisson | |||
##Introdução à teoria das filas | |||
{{collapse bottom}} | |||
{{collapse top | Semestre 2014-2 - Prof. Roberto Nóbrega}} | |||
# Revisão de teoria da probabilidade e variáveis aleatórias | |||
## Teoria da probabilidade | |||
## Variáveis aleatórias contínuas e discretas | |||
## Funções massa, densidade e cumulativa | |||
## Esperança matemática (média, variância, momentos) | |||
## Função característica | |||
## Variáveis aleatórias conjuntas | |||
## Probabilidade condicional e o Teorema de Bayes | |||
## Vetores aleatórios | |||
# Definição e classificação de processos estocásticos | |||
## Definição e especificação de processos estocásticos | |||
## Processos contínuos e discretos | |||
## Estacionariedade e ergodicidade | |||
## Exemplos de processos estocásticos | |||
# Processos estocásticos estacionários no sentido amplo | |||
## Função de autocorrelação | |||
## Densidade espectral de potência | |||
## Resposta de sistemas lineares a entradas aleatórias | |||
## Processos auto-regressivos e de média-móvel | |||
## Processos gaussianos | |||
# Processos de Poisson e cadeias de Markov | |||
## Processos de Poisson | |||
## Cadeias de Markov | |||
## Introdução à teoria das filas | |||
# Processos de Wiener e caminhadas aleatórias | |||
{{collapse bottom}} | |||
;Estratégias de ensino utilizadas | ;Estratégias de ensino utilizadas | ||
* Aulas expositivas teóricas. | |||
* Listas de exercícios extraclasses. | |||
* Atividades de simulação computacional. | |||
;Critérios e instrumentos de avaliação | ;Critérios e instrumentos de avaliação | ||
* Três provas teóricas escritas. | |||
* Um trabalho de simulação computacional. | |||
;Bibliografia Básica | ;Bibliografia Básica | ||
# | # Jose Paulo de Almeida e Albuquerque, Jose Mauro Pedro Fortes, Weiler Alves Finamore '''Probabilidade, Variáveis e Processos Estocásticos'''; 1ª ed. [S.l]:Interciência, 2008. 334p. ISBN 9788571931909 | ||
# | # Roy D. Yates and David J. Goodman '''Probability and Stochastic Processes: A Friendly Introduction for Electrical and Computer Engineers'''; 3ª ed. [S.l]:Wiley, 2014. 512p. ISBN 9781118324561 | ||
# | # Marcelo Sampaio de Alencar '''Probabilidade e Processos Estocásticos'''; 1ª ed. [S.l]:Erica, 2009. 288p. ISBN 9788536502168 | ||
;Bibliografia Complementar | ;Bibliografia Complementar | ||
# | # Papoulis, Athanasios '''Probability, Random Variables and Stochastic Processes'''; 4ª ed. Boston:McGraw-Hill, 2002. 852p. ISBN 9780071226615 | ||
# Steven Kay '''Intuitive Probability and Random Processes using MATLAB'''; ed. [S.l]:Springer, 2006. p. ISBN 9780387241579 | |||
# Hwei Hsu '''Schaum's Outline of Probability, Random Variables, and Random Processes'''; 2ª ed. [S.l]:McGraw-Hill, 2010. p. ISBN 9780071632898 | # Hwei Hsu '''Schaum's Outline of Probability, Random Variables, and Random Processes'''; 2ª ed. [S.l]:McGraw-Hill, 2010. p. ISBN 9780071632898 | ||
# Stewart, William J. '''Probability, markov chains, queues, and simulation : the mathematical basis of performance modeling'''; ed. New Jersey:Princeton University Press, 2009. 776p. ISBN 9780691140629 | # Stewart, William J. '''Probability, markov chains, queues, and simulation : the mathematical basis of performance modeling'''; ed. New Jersey:Princeton University Press, 2009. 776p. ISBN 9780691140629 | ||
# Henry Stark, John Woods '''Probability, Statistics, and Random Processes for Engineers'''; 4ª ed. [S.l]:Prentice Hall, 2011. 704p. ISBN 9780132311236 | # Henry Stark, John Woods '''Probability, Statistics, and Random Processes for Engineers'''; 4ª ed. [S.l]:Prentice Hall, 2011. 704p. ISBN 9780132311236 | ||
Edição atual tal como às 13h10min de 22 de março de 2016

|
MINISTÉRIO DA EDUCAÇÃO |
Plano de Ensino de 2014-2 - atual
- Dados gerais
- COMPONENTE CURRICULAR: PRE - PROCESSOS ESTOCÁSTICOS
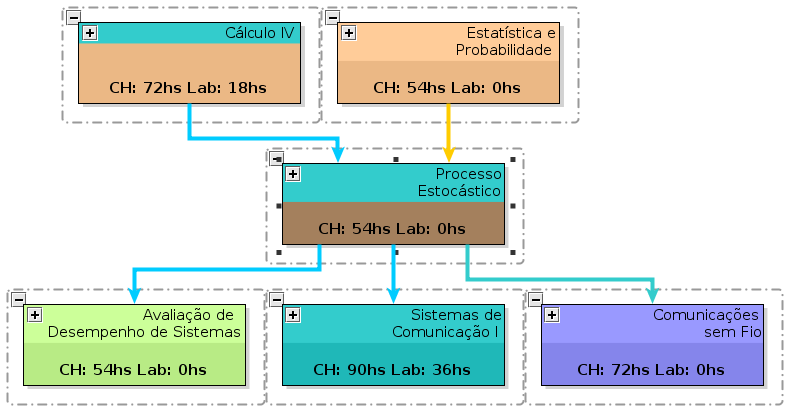
- CARGA HORÁRIA: 3 HORAS/SEMANA 54 HORAS. TEÓRICA = 54 HORAS. LABORATÓRIO = 0 HORAS
- PRÉ REQUISITOS: EST, CAL4
- DISCIPLINAS SUCESSORAS: CSF, ADS, COM1
- MÓDULO PROFISSIONALIZANTE
- Ementa
- Variáveis aleatórias. Definição e classificação de processo estocásticos. Processos contínuos e discretos no tempo. Classes de processos estocásticos. Processos Random Walk e Wiener. Processos de Poisson. Estacionariedade. Autocorrelação e representação espectral. Continuidade, Diferenciação e Integração. Ergodicidade e média no tempo. Decomposição espectral e expansão em séries. Resposta de sistemas lineares a entradas aleatórias. Processos Estocásticos especiais: processos autoregressivos, modelos “moving average”. Processos e sequências de Markov. Processos Gaussianos. Aplicação de processos estocásticos em Telecomunicações.
- Objetivos
- Conhecer os fundamentos da teoria da probabilidade, variáveis aleatórias e processos estocásticos.
- Saber modelar e solucionar problemas de natureza probabilística, em particular aqueles com aplicações na área de telecomunicações.
- Possuir conhecimento básico sobre a simulação em computador de experimentos probabilísticos.
- Conteúdo Programático
| Semestre 2016-1 - Prof. Roberto Nóbrega |
|---|
|
| Semestre 2015-2 - Prof. Roberto Nóbrega |
|---|
|
| Semestre 2015-1 - Prof. Roberto Nóbrega |
|---|
|
| Semestre 2014-2 - Prof. Roberto Nóbrega |
|---|
|
- Estratégias de ensino utilizadas
- Aulas expositivas teóricas.
- Listas de exercícios extraclasses.
- Atividades de simulação computacional.
- Critérios e instrumentos de avaliação
- Três provas teóricas escritas.
- Um trabalho de simulação computacional.
- Bibliografia Básica
- Jose Paulo de Almeida e Albuquerque, Jose Mauro Pedro Fortes, Weiler Alves Finamore Probabilidade, Variáveis e Processos Estocásticos; 1ª ed. [S.l]:Interciência, 2008. 334p. ISBN 9788571931909
- Roy D. Yates and David J. Goodman Probability and Stochastic Processes: A Friendly Introduction for Electrical and Computer Engineers; 3ª ed. [S.l]:Wiley, 2014. 512p. ISBN 9781118324561
- Marcelo Sampaio de Alencar Probabilidade e Processos Estocásticos; 1ª ed. [S.l]:Erica, 2009. 288p. ISBN 9788536502168
- Bibliografia Complementar
- Papoulis, Athanasios Probability, Random Variables and Stochastic Processes; 4ª ed. Boston:McGraw-Hill, 2002. 852p. ISBN 9780071226615
- Steven Kay Intuitive Probability and Random Processes using MATLAB; ed. [S.l]:Springer, 2006. p. ISBN 9780387241579
- Hwei Hsu Schaum's Outline of Probability, Random Variables, and Random Processes; 2ª ed. [S.l]:McGraw-Hill, 2010. p. ISBN 9780071632898
- Stewart, William J. Probability, markov chains, queues, and simulation : the mathematical basis of performance modeling; ed. New Jersey:Princeton University Press, 2009. 776p. ISBN 9780691140629
- Henry Stark, John Woods Probability, Statistics, and Random Processes for Engineers; 4ª ed. [S.l]:Prentice Hall, 2011. 704p. ISBN 9780132311236
1 ANEXOS