Aula 1 (ELM3605)

1 Introdução e Histórico

Primeiros meios de telecomunicação: Telégrafo , Rádiodifusão Principais problemas --> raios --> possuem amplo espectro de frequência

Surgiam as linhas de transmissão de energia elétrica: grandes fontes de irradiação em baixa freqüencia e alta potência.

1.1 Entradas de interferência

Rede elétrica Antenas

1.2 Estudos CEM (EMC)

os equipamentos não devem interferir em outros;

os equipamentos não devem sofrer interferências externas;

os equipamentos não devem causar interferências em si próprios;

1.3 Ruídos

• Ruído conduzido: 150 KHz à 30 MHz
• Ruído irradiado: 30 MHz à 30 GHz

ESD descarga (Raio) EMP pulso (espectro infinito)

1.4 Análise vetorial

Todos os fenômenos eletromagnéticos são descritos pelas equações de Maxwell. Ao ponto de vista matemático é um pouco complexo, mas muito útil.

Análise Vetorial

As equações de Maxwell descrevem termos em um espaço tridimensional. As quantidades dos campos são descritos por vetor quantidade simbolizado por :

• para facilitar a representação usarei ^ em vez de flecha para representação vetorial

 . |Â| = A módulo

O vetor descrito em um sistema de coordenadas cartesianas ou retangulares.

P1 = [ x1 ; y1 ; z1 ]

 = Ax âx + Ay ây + Az âz

1.5 Diferenciais

Caminho ou linha:

∂ℓ = ∂x âx + ∂y ây + ∂z âz

Área:

∂S = dy dz âx + dx dz ây + dx dy âz

Volume:

∂v = dx dy dz

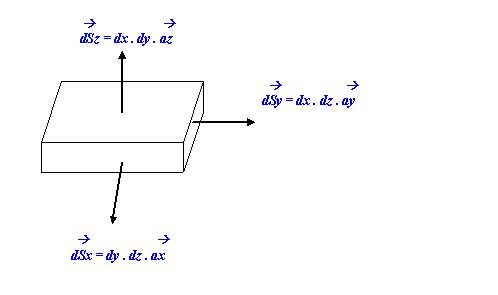
1.6 Produto Escalar

 . B = |Â| . |B| cos theta AB

1.7 Produto Vetorial

 . B = |Â| . |B| sen theta AB . ân

1.8 Integral de Linha de um Campo Vetorial

∫c F . dl = ∫c (F) cos theta dl =

∫cx Fx dx + ∫cy Fy dy + ∫cz Fz dz EQ. 01

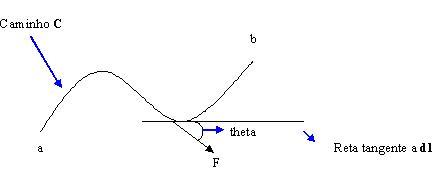
A EQ. 01 soma (integra) o produto da componente de F tangente ao caminho de (|F| cos theta)

1.9 Exemplo

Determinar o trabalho necessário para mover um objeto do ponto P1 até o P2 no campo vetorial F ao longo da trajetória de P1 para P2:

P1 = [1,1,0] (m)

P2 = [0,2,3] (m)

F = 2 y ax + x y ay + z az

Solução:

w = - ∫ F dl (integrar de P1 até P2)

w = (∫(integrar de 1 a 0) 2 y dx + ∫(integrar de 1 a 2) x y dy + ∫(integrar de 0 a 3) z dz)

y = - x + z

x = - y + 2

w = -13/6 J

1.10 Exercício

Resolver integral de linha de F = 2y . ax + 3x . ay + az do ponto [0,0,0] até o [1,2,3].

∫F∂l = ∫Fx∂x + ∫Fy∂y + ∫Fz∂z

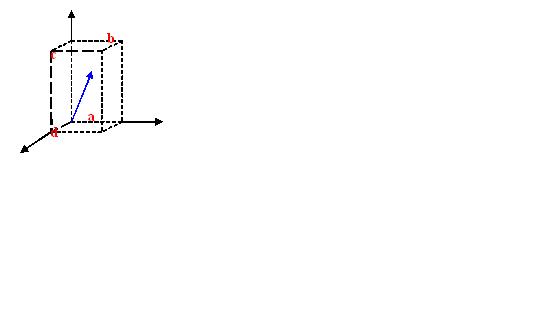
do ponto a -> d ∫(0→1) 2y∂x + ∫(0→0) 3x∂y + ∫(0→0)∂z = 2yx |(0→1) = 2y = 0

do ponto d -> c ∫(0→3) dz = 3

do ponto c -> b ∫(0→2) 3x∂y = 3xy |(0→2) = 3x . 2 - 3x . 0 = 6x = 6

Então:

3 + 6 = 9

Simbolos para facilitar .. ƒβεθλΨΩω∞∂ℓ∫≈≠≤≥α→ Página de Ajuda da Wikipedia