CEL018702 2019 1 AULA07: mudanças entre as edições
Sem resumo de edição |
|||
| Linha 40: | Linha 40: | ||
Resistência equivalente (R): | Resistência equivalente (R): | ||
<math>\frac{1}{R}=\frac{1}{10}+\frac{1}{2}=1,667 \Omega\,</math> | <math>\frac{1}{R}=\frac{1}{10}+\frac{1}{2}\to R=1,667 \Omega\,</math> | ||
<math>V_M=I.R=2,8.1,667=4,67 V\,</math> | <math>V_M=I.R=2,8.1,667=4,67 V\,</math> | ||
Edição atual tal como às 15h50min de 25 de abril de 2019
1 Teorema de Millman
O Teorema de Millman apresenta um método usado para reduzir um número qualquer de fontes de tensão em paralelo a apenas uma. Este teorema constitui um caso especial da aplicação do teorema de Thévenin. A Figura 1 apresenta um exemplo de simplificação utilização o teorema de Millman.
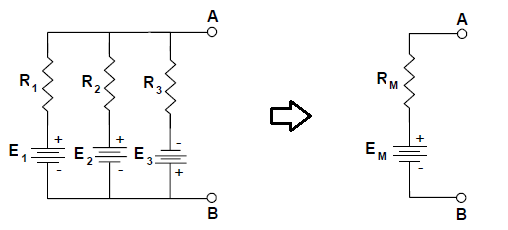
Figura 1 - Teorema de Millman para simplificação de fontes de tensão.
O primeiro passo é transformar as fontes de tensão com resistência em série em fontes de corrente com resistências em paralelo. A seguir, deve-se calcular o circuito equivalente com uma única fonte de corrente e uma única resistência. Estes cálculos são feitos da seguinte maneira:
A transformação do circuito fonte de corrente e resistência em paralelo em fonte de tensão e resistência em série deve ser realizada da seguinte maneira:
1.1 Exemplo
Determinar a corrente na resistência de 5 ohms utilizando o teorema de Millman. Confirme os resultados utilizando o teorema de Thevenin.
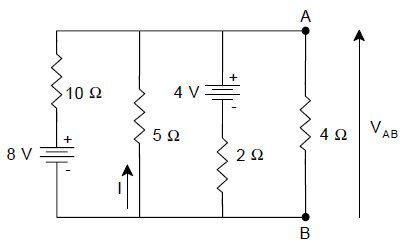
| Solução |
|---|
Corrente (I):
Resistência equivalente (R):
Logo:
|
2 Associação de Fontes
2.1 Fontes de Tensão
A associação em série de fontes de tensão permite aumentar a diferença de potencial disponibilizada para efeitos de alimentação de um circuito. Um exemplo da associação em série de fontes é a utilização de múltiplas pilhas para alimentar aparelhos eletrodomésticos como lanternas, rádios portáteis. Com efeito, é comum associarem-se em série quatro pilhas de 1.5 V (corretamente associadas) para definir uma fonte de alimentação de 6 V.
A tensão disponível aos terminais de uma associação em série de fontes de tensão é dada pela soma das tensões parciais. Como se indica nas Figuras 2 (a) e 2 (b), a adição dos valores nominais das tensões deve ter em conta a polaridade da ligação: polaridades concordantes adicionam-se (a), e polaridades discordantes subtraem-se (b). Por outro lado, no caso das fontes de tensão com resistência interna não nula, como na Figura 2 (c), o valor da resistência interna resultante é dado pela soma das resistências internas de cada uma das fontes. A associação em série conduz, por conseguinte, a uma fonte cuja resistência interna é superior àquela característica de cada uma, considerada isoladamente.
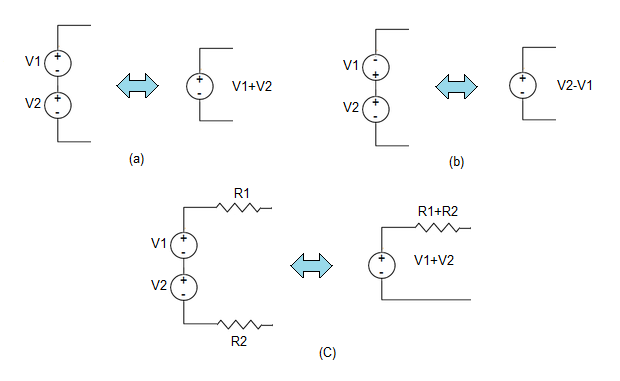
Figura 2 - Associação em série de fontes de tensão.
A associação em paralelo de fontes de tensão é uma operação cuja realização prática necessita de alguns cuidados. Esta recomendação é particularmente verdadeira nos casos em que as fontes de tensão apresentam valores nominais bastante diferenciados e resistências internas reduzidas. Como se ilustra na Figura 3 (a), no caso particular em que as fontes de tensão são ideais e apresentam valores nominais distintos, a sua ligação em paralelo define uma malha cuja solução é apenas compatível com a circulação de uma corrente de valor infinito. Na realidade, a corrente entre as fontes é sempre limitada pelas respectivas resistências internas Figura 3 (b), valor que pode ser bastante elevado se estas não dispuserem de mecanismos de proteção.
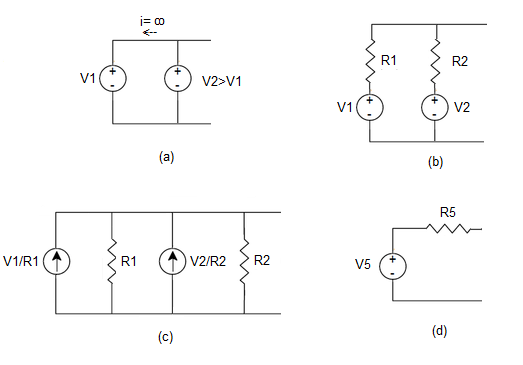
Figura 3 - Associação em paralelo de fontes de tensão.
A associação em paralelo de fontes de tensão é o objeto do Teorema de Millman. De acordo com as regras estabelecidas para a transformação de fonte, o circuito representado na Figura 3 (b) pode ser sucessivamente transformado nos circuitos equivalentes representados em (c) e (d). Na primeira transformação, Figura 3 (c), substitui-se cada uma das fontes de tensão pela respectiva fonte de corrente equivalente, efetuando-se depois, sucessivamente, as associações em paralelo das fontes de corrente e das resistências internas, e a transformação inversa numa fonte de tensão com resistência interna. É facilmente demonstrável que os parâmetros da fonte de tensão resultante são:
e
respectivamente para o valor nominal da tensão e para a resistência interna.
2.2 Fonte de Corrente
A associação em paralelo de fontes de corrente rege-se por um conjunto de regras semelhante àquele estabelecido para a associação em série de fontes de tensão. Neste caso, a corrente colocada aos terminais de uma associação em paralelo é dada pela soma das correntes parciais (Figura 4.a e 4.b), que naturalmente deve ter em conta as polaridades respectivas. No caso das fontes de corrente reais, Figura 4.16.c, o valor da resistência interna é dada pelo paralelo das resistências internas parciais, o que torna a fonte de corrente mais acentuadamente não ideal.
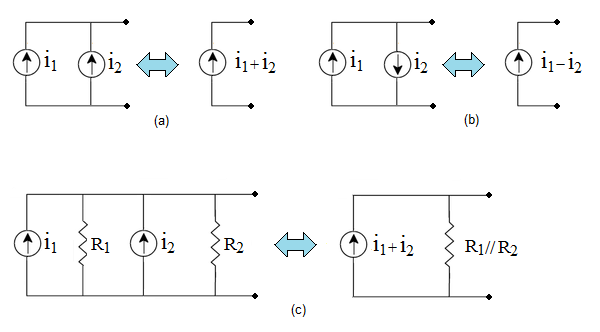
Figura 4 - Associação em paralelo de fontes de corrente.
- Nota
- A associação em série de fontes de corrente ideais com valores nominais distintos conduz a uma indeterminação no nó de interligação, devido a não verificação da Lei de Kirchhoff das correntes. No nó comum às duas fontes deve verificar-se sempre a igualdade i1-i2=0, ou, o que é o mesmo, i1=i2.
3 Princípio da Superposição
O teorema da superposição para circuitos elétricos afirma que a corrente elétrica total em qualquer ramo de um circuito bilateral linear é igual a soma algébrica das correntes produzidas por cada fonte atuando separadamente no circuito. Isto vale também para tensões elétricas.
3.1 Video aula
3.2 Exemplo
Superposição (Sistemas Lineares)
A resposta de um circuito linear a várias excitações simultâneas é igual à soma das respostas individuais a cada uma das excitações.
Procedimento:
1. Calcula-se a solução para o estado inicial, anulando-se as entradas (curto-circuitando as fontes de tensão e abrindo as fontes de corrente).
2. Calcula-se a solução para cada fonte, anulando-se as condições iniciais e as demais fontes do circuito.
3. Somam-se as soluções individuais.
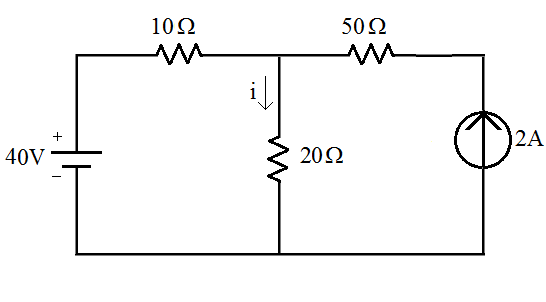
Figura 1 - Circuito original com uma fonte de tensão e outra de corrente.
- Determinar a corrente i
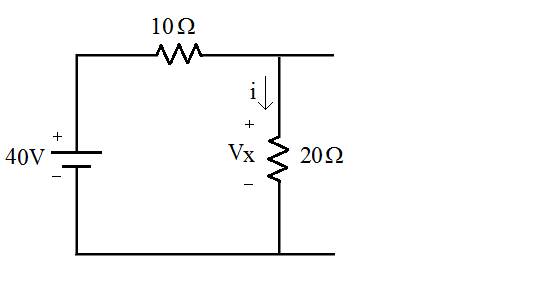
Figura 2 - Circuito a partir da fonte de tensão.
- Fonte de tensão
| Solução |
|---|
|
|
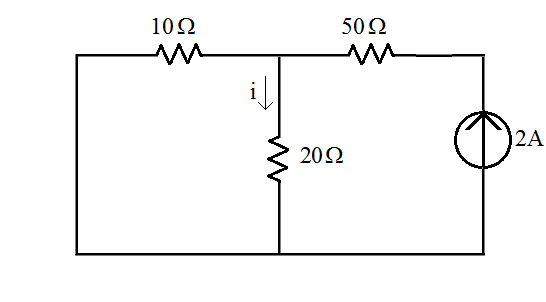
Figura 3 - Circuito a partir da fonte de corrente.
- Fonte de corrente
| Solução |
|---|
|
|
- Resultado
| Solução |
|---|
|
|
- Verificação através da análise de malha
| Solução |
|---|
|
Como:
|
4 Exercícios
4.1 Superposição
[1] Determinar a Corrente I no circuito abaixo usando o teorema da Superposição.
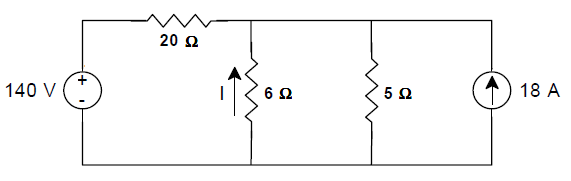
[2] Qual a corrente sobre o resistor de 12 ohms?
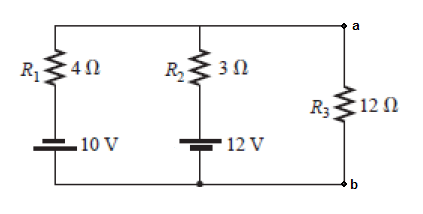
[3] Para o circuito abaixo, calcule o valor da tensão V0, utilizando:
a) O Teorema de de Thevenin (5 escores)
b) O Princípio da Superposição (5 escores)
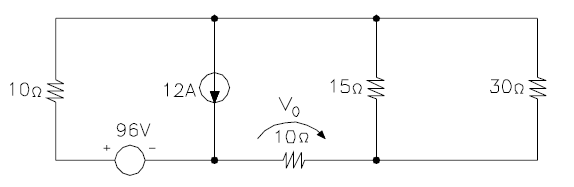
| Resposta |
|---|
|
V0=-8V |
[4] Para o circuito abaixo, calcule o valor da corrente I0, utilizando:
a) O Teorema de de Thevenin (5 escores)
b) O Princípio da Superposição (5 escores)

| Resposta |
|---|
|
I0=-1A |
[5] Para o circuito abaixo, calcule o valor da tensão V0, utilizando:
a) O Teorema de de Thevenin (5 escores)
b) O Princípio da Superposição (5 escores)
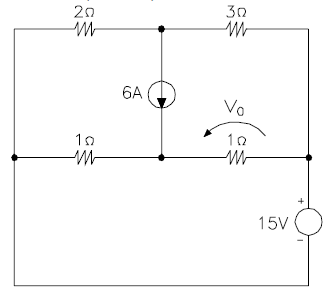
| Resposta |
|---|
|
V0=-4,5V (confirmar) |
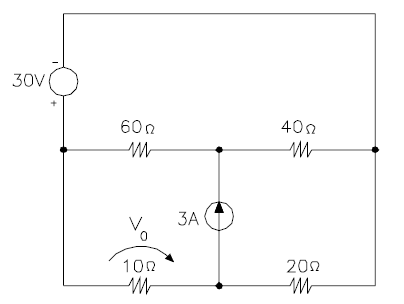
[6] Para o circuito abaixo, calcule o valor da tensão V0, utilizando:
a) O Teorema de de Thevenin (5 escores)
b) O Princípio da Superposição (5 escores)
| Resposta |
|---|
|
V0=-30V (confirmar) |
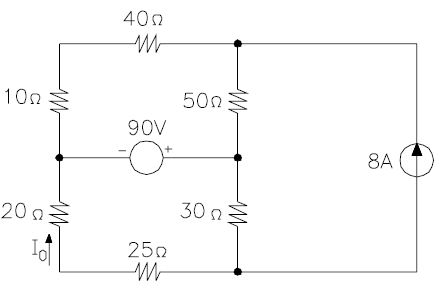
[7] Para o circuito abaixo, calcule o valor da corrente I0, utilizando:
a) O Teorema de de Thevenin (5 escores)
b) O Princípio da Superposição (5 escores)
| Resposta |
|---|
|
I0=-2A |
4.2 Millman
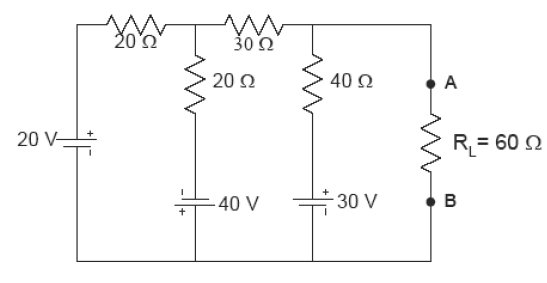
[1] Calcule, utilizando o teorema de Millman, o circuito equivalente ao circuito dado, visto de (A e B). Calcule tensão e corrente em .
| Solução |
|---|
|
|
[2] Calcule VAB com o circuito em aberto e depois com Rc=3Ω ligada ao circuito.

| Respostas |
|---|
|
VTh=4,2V; RTh=RN=3Ω; IN=1,4A; VAB=2,1V |
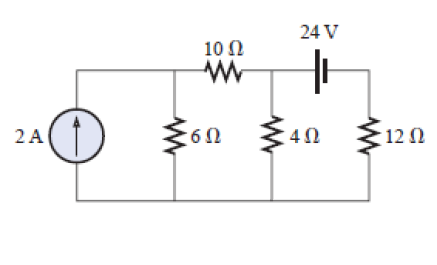
[3] Calcule a tensão sobre o resistor de 4Ω.
| Respostas |
|---|
|
|
[4] Calcule a tensão sobre o resistor de 6Ω.
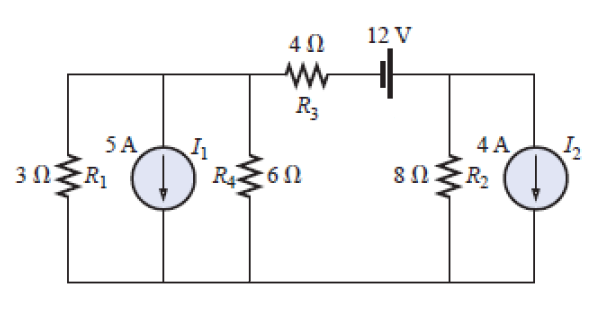
| Respostas |
|---|
|
|
[5] Utilizando o método dos nós calcular a corrente I0 para o circuito abaixo.
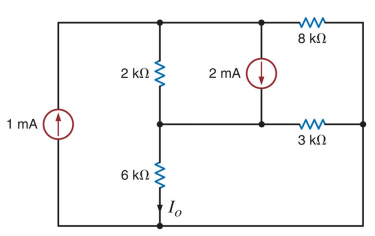
| Respostas |
|---|
|
I0=0,33uA |
[6] Utilizando análise de nós, determine o valor de VX para o circuito abaixo.
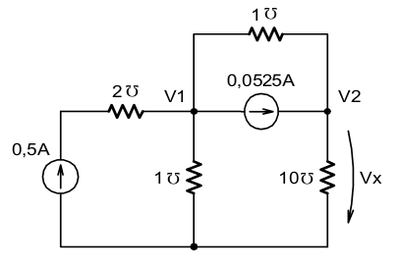
| Respostas |
|---|
|
VX=26,3mV |
[7] Determine os equivalentes de Thévenin e de Norton do circuito abaixo. Calcule VAB com Rc=3Ω ligada ao circuito.

| Respostas |
|---|
|
VTh=4,2V; RTh=RN=3Ω; IN=1,4A; VAB=2,1V |
[8] Calcule os equivalentes de Thévenin e de Norton para o circuito abaixo. Calcule VAB com RL ligada ao circuito.
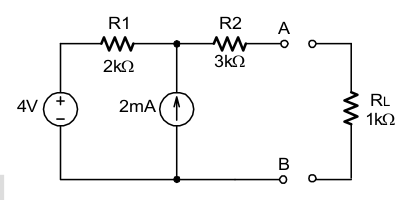
| Solução |
|---|
Só existe uma malha de corrente no circuito e é a de 2mA. Lembre-se que entre A e B está aberto.Como não há corrente circulando pelo R2, a tensão VAB é a soma da queda de tensão no resistor R1 mais a fonte de 4V. Sabendo que a corrente de malha é 2mA fica:
Para calcular a resistência equivalente a fonte de corrente fica em aberto enquanto a fonte de tensão fica em curto, logo:
Colocando de volta o resistor da carga RL, o VAB que é a tensão sobre a carga fica:
então, o novo VAB é
VTh=8V; RTh=RN=5kΩ; IN=1,60mA; VAB=-1,33V
Pessoal, como não gosto de deixar coisas mal resolvidas, vejam como fica a análise principal do circuito, com Norton, utilizando a Lei de Kirchoff (foi aí que "erramos"). O sentido da corrente i1 é entrando no nó, juntamente com a corrente de 2mA. Logo, a corrente i2 que sai do nó é soma de i1 mais 2mA. Vejam como fica: Equação 1:
Equação 2: (passando pela malha de fora)
Daí é só fazer os outros cálculos.
|
5 Referências
[1] http://www.corradi.junior.nom.br/teoremas_exer_resolvido.pdf
[2] http://www.ufrgs.br/eng04030/Aulas/teoria/cap_04/assocfon.htm
[3] http://www.dt.fee.unicamp.br/~www/ea612/node140.html