CEL18702 2017 1 AULA12

1 Objetivos

• Preparar-se para a AT2
• Exercitar Análise Nodal
• Exercitar Equivalentes de Thevenin e Norton

2 Lista de Exercícios

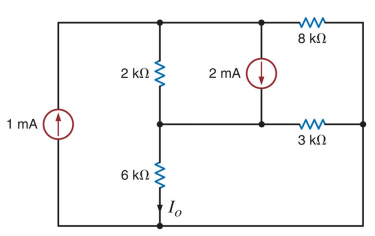
[1] Utilizando o método dos nós calcular a corrente I₀ para o circuito abaixo.

Respostas
I0=0,33uA

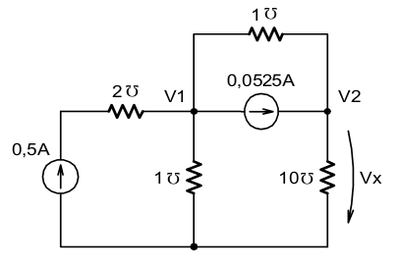
[2] Utilizando análise de nós, determine o valor de V_X para o circuito abaixo.

Respostas
VX=26,3mV

[3] Determine os equivalentes de Thévenin e de Norton do circuito abaixo. Calcule V_AB com R_c=3Ω ligada ao circuito.

Respostas
VTh=4,2V; RTh=RN=3Ω; IN=1,4A; VAB=2,1V

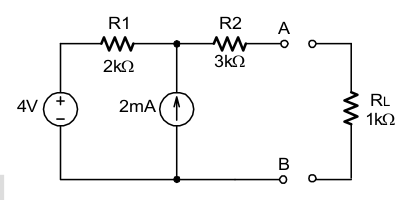
[4] Calcule os equivalentes de Thévenin e de Norton para o circuito abaixo. Calcule V_AB com R_L ligada ao circuito.

Solução

Thevenin Só existe uma malha de corrente no circuito e é a de 2mA. Lembre-se que entre A e B está aberto.Como não há corrente circulando pelo R2, a tensão VAB é a soma da queda de tensão no resistor R1 mais a fonte de 4V. Sabendo que a corrente de malha é 2mA fica: $V_{AB}=R_1.2.10^{-3}+4$ $V_{AB}=2.10^3.2.10^{-3}+4$ $V_{AB}=V_{Th}=8V$ Para calcular a resistência equivalente a fonte de corrente fica em aberto enquanto a fonte de tensão fica em curto, logo: $R_{eq}=2k+3k=5k\mathrm{\Omega }$ $R_{eq}=R_{Th}=5k\mathrm{\Omega }$ Para calcular o IN fazemos: $I_N=\frac{V_{Th}}{R_{Th}}=\frac{8}{5.10^3}=1,6mA$ Colocando de volta o resistor da carga RL, o VAB que é a tensão sobre a carga fica: $I_L=\frac{V_{Th}}{R_{Th}+R_L}=\frac{8}{5.10^3+1.10^3}=1,33mA$ então, o novo VAB é $V_{AB}=R_L.I_L=1.10^3.1,33.10^{-3}=1,33V$ Confirmando todos os resutados: VTh=8V; RTh=RN=5kΩ; IN=1,60mA; VAB=-1,33V Norton Pessoal, como não gosto de deixar coisas mal resolvidas, vejam como fica a análise principal do circuito, com Norton, utilizando a Lei de Kirchoff (foi aí que "erramos"). O sentido da corrente i1 é entrando no nó, juntamente com a corrente de 2mA. Logo, a corrente i2 que sai do nó é soma de i1 mais 2mA. Vejam como fica: Equação 1: $i_2=i_1+2.10^{-3}$ Logo, $-i_1+i_2=2.10^{-3}$ Equação 2: (passando pela malha de fora) $-4+2.10^3{i}_1+3.10^3{i}_2=0$ $2.10^3{i}_1+3.10^3{i}_2=4$ Resolvendo o sistema (Cramer) $\mathrm{\Delta }=\left|\begin{array}{cc}-1& 1\\ 2.10^3& 3.10^3\end{array}\right|.\left|\begin{array}{c}2.10^{-3}\\ 4\end{array}\right|$ $\mathrm{\Delta }=\left|\begin{array}{cc}-1& 1\\ 2.10^3& 3.10^3\end{array}\right|=-3.10^3-2.10^3\mathrm{\Delta }=-5.10^3$ $\mathrm{\Delta }{i}_2=\left|\begin{array}{cc}-1& 2.10^{-3}\\ 2.10^3& 4\end{array}\right|=-4-4\mathrm{\Delta }{i}_2=-8$ $i_2=\frac{\mathrm{\Delta }{i}_2}{\mathrm{\Delta }}=\frac{-8}{-5.10^3}{i}_2=1,6mA$ Daí é só fazer os outros cálculos. Prof. Douglas A.

---