EDI018702 2020 2 AULA02: mudanças entre as edições
| (18 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
= | =Apresentação= | ||
Os flip-flops são | Os contadores são circuitos que utilizam flip-flops e são aplicados, principalmente, em contagens, diversas, divisão de frequência, medição de frequência e tempo, divisão de formas de onda e conversão de analógico para digital. Estes circuitos sequenciais são divididos basicamente em duas categorias: | ||
*Contadores assíncronos; e | |||
*Contadores síncronos. | |||
Basicamente a principal diferença entre eles é que o síncrono utiliza um sinal de ''clock'' comum a todos os flip-flops e o assíncrono possuí um sinal de ''clock'' que é dividido até o último flip-flops. | |||
=Contadores Assíncronos= | |||
Estes contadores também são conhecidos como seriais ou contadores por pulsação (''ripple counter''). Tal nome advém do fato dos flip-flops (FF) do contador não serem disparados diretamente pelo sinal de ''clock''. Cada FF é disparado pela saída do FF anterior. Esta característica torna estes contadores limitados em termos de velocidade, pois o tempo de ativação (tempo de resposta) é dado aproximadamente pela soma dos tempos de atraso de propagação de cada FF. | |||
é | |||
==Crescente== | |||
[[Imagem: | Um circuito típico de um contador assíncrono crescente construído com FF do tipo JK é mostrado na Figura 1. Os FF JK estão com ambas entradas J e K permanentemente em nível alto, estando configuradas portanto como FF tipo T. Cada FF é disparado pela saída do FF anterior. A Figura 2 mostra o diagrama de tempo para esse contador. | ||
[[Imagem:fig14_DIG222802.png|center|500px]] | |||
<center> | |||
Figura 1 - Contador assíncrono crescente. | |||
</center> | |||
[[Imagem:fig15_DIG222802.png|center|600px]] | |||
<center> | <center> | ||
Figura | Figura 2 - Diagrama de tempo do contador assíncrono crescente. | ||
</center> | </center> | ||
{| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | |||
|+'''Tabela 1 - Contador assíncrono crescente MOD-16''' | |||
|- | |||
! style="background:#6A5ACD; color:white; width: 20px;" | Clock | |||
! style="background:#6A5ACD; color:white; width: 20px;" | D | |||
! style="background:#6A5ACD; color:white; width: 20px;" | C | |||
! style="background:#6A5ACD; color:white; width: 20px;" | B | |||
! style="background:#6A5ACD; color:white; width: 20px;" | A | |||
! style="background:#6A5ACD; color:white; width: 20px;" | Decimal | |||
! style="background:#6A5ACD; color:white; width: 20px;" | Estado | |||
|- | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
|- | |||
| 1 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 1 | |||
| 1 | |||
| 1 | |||
|- | |||
| 2 | |||
| 0 | |||
| 0 | |||
| 1 | |||
| 0 | |||
| 2 | |||
| 2 | |||
|- | |||
| 3 | |||
| 0 | |||
| 0 | |||
| 1 | |||
| 1 | |||
| 3 | |||
| 3 | |||
|- | |||
| 4 | |||
| 0 | |||
| 1 | |||
| 0 | |||
| 0 | |||
| 4 | |||
| 4 | |||
|- | |||
| 5 | |||
| 0 | |||
| 1 | |||
| 0 | |||
| 1 | |||
| 5 | |||
| 5 | |||
|- | |||
| 6 | |||
| 0 | |||
| 1 | |||
| 1 | |||
| 0 | |||
| 6 | |||
| 6 | |||
|- | |||
| 7 | |||
| 0 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 7 | |||
| 7 | |||
|- | |||
| 8 | |||
| 1 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 8 | |||
| 8 | |||
|- | |||
| 9 | |||
| 1 | |||
| 0 | |||
| 0 | |||
| 1 | |||
| 9 | |||
| 9 | |||
|- | |||
| 10 | |||
| 1 | |||
| 0 | |||
| 1 | |||
| 0 | |||
| 10 | |||
| 10 | |||
|- | |||
| 11 | |||
| 1 | |||
| 0 | |||
| 1 | |||
| 1 | |||
| 11 | |||
| 11 | |||
|- | |||
| 12 | |||
| 1 | |||
| 1 | |||
| 0 | |||
| 0 | |||
| 12 | |||
| 12 | |||
|- | |||
| 13 | |||
| 1 | |||
| 1 | |||
| 0 | |||
| 1 | |||
| 13 | |||
| 13 | |||
|- | |||
| 14 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 0 | |||
| 14 | |||
| 14 | |||
|- | |||
| 15 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 15 | |||
| 15 | |||
|- | |||
| 16 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
|- | |||
| 17 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 1 | |||
| 1 | |||
| 1 | |||
|- | |||
| 18 | |||
| 0 | |||
| 0 | |||
| 1 | |||
| 0 | |||
| 2 | |||
| 2 | |||
|} | |||
O contador tem como conteúdo (estado interno) a contagem do número de transições negativas do ''clock'', de forma que quando ocorre uma transição o conteúdo é incrementado de uma unidade. O conteúdo do contador é dado pelo número binário DCBA, onde A é o bit LSB (bit menos significativo) e D é o bit MSB (bit mais significativo). | |||
< | O modulo (MOD) de um contador é o seu número de estados distintos, portanto, o módulo de um contador com N FF pode ser no máximo o número de possíveis saídas (<math>2^N</math>). A Tabela mostra os estados de contagem de um contador assíncrono com 4 FF (4 bits). Podemos perceber que após 16 transições de ''clock'' o contador reinicia a contagem. Por isso, este contador é de MOD-16, ou seja, tem 16 estados distintos (0000b até 1111b). | ||
Nos contadores assíncronos, a frequência do ''clock'' é dividida por 2 em cada FF, ou seja: na saída A temos ''clock/2'', e na saída D temos ''clock/16''. Portanto, os contadores assíncronos são divisores de frequência e no último FF a frequência de ''clock'' é dividida pelo módulo do contador. | |||
{{collapse top|Circuito do Contador Assíncrono de 3 bits - ''falstad''}} | |||
Na página do falstad, copiar o código abaixo e colar em: Arquivo->Importar arquivo de texto... | |||
<pre> | |||
$ 1 0.000005 10.20027730826997 50 5 43 | |||
156 96 96 176 96 0 5 | |||
</ | 156 256 96 272 96 0 5 | ||
156 416 96 448 96 0 0 | |||
L 96 96 64 96 2 1 false 5 0 | |||
L 96 160 64 160 2 1 false 5 0 | |||
L 256 96 240 96 2 1 false 5 0 | |||
L 256 160 240 160 2 1 false 5 0 | |||
L 416 96 400 96 2 1 false 5 0 | |||
L 416 160 400 160 2 1 false 5 0 | |||
M 192 96 192 32 2 2.5 | |||
M 352 96 352 32 2 2.5 | |||
M 512 96 512 32 2 2.5 | |||
R 96 128 48 128 1 2 100 2.5 2.5 0 0.5 | |||
w 256 128 192 96 0 | |||
w 416 128 352 96 0 | |||
403 0 240 544 288 0 12_64_0_4099_5_0.00009765625_0_2_12_3 | |||
403 0 288 544 320 0 9_64_0_4098_5_0.1_0_1 | |||
403 0 336 544 368 0 10_64_0_4098_5_0.1_0_1 | |||
403 0 384 544 416 0 11_64_0_4098_5_0.1_0_1 | |||
</pre> | |||
{{collapse bottom}} | |||
==Contadores de Módulo== | |||
Para obter um contador com módulo menor do que <math>2^N</math> é necessário adicionar um circuito decodificador para reiniciar a contagem antes de chegar ao valor máximo (ou mínimo). A Figura 3 mostra um contador MOD-6. Se não houvesse a porta NAND ligada nas entradas CLR dos FF o módulo do contador seria 8. A sequência de estados do contador MOD-6 é mostrada nas Figura 4 e Tabela 2. Note que na transição do 6º ''clock'' o estado do contador passa temporariamente pelo estado (110b), o qual faz com que a saída da porta NAND passe para o estado BAIXO, causando o CLR nos FF, e consequentemente levando o contador para o estado (000b). | |||
[[Imagem:fig16_DIG222802.png|center|500px]] | |||
<center> | |||
Figura 3 - Contador assíncrono com módulo < <math>2^N</math>. | |||
</center> | |||
[[Imagem: | [[Imagem:fig17_DIG222802.png|center|600px]] | ||
<center> | <center> | ||
Figura 4 - | Figura 4 - Diagrama de tempo do contador com módulo < <math>2^N</math>. | ||
</center> | </center> | ||
{| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
|+''' | |+'''Tabela 2 - Contador assíncrono crescente MOD-6''' | ||
|- | |||
! style="background:#6A5ACD; color:white; width: 20px;" | Clock | |||
! style="background:#6A5ACD; color:white; width: 20px;" | C | |||
! style="background:#6A5ACD; color:white; width: 20px;" | B | |||
! style="background:#6A5ACD; color:white; width: 20px;" | A | |||
! style="background:#6A5ACD; color:white; width: 20px;" | Decimal | |||
! style="background:#6A5ACD; color:white; width: 20px;" | Estado | |||
|- | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
|- | |||
| 1 | |||
| 0 | |||
| 0 | |||
| 1 | |||
| 1 | |||
| 1 | |||
|- | |||
| 2 | |||
| 0 | |||
| 1 | |||
| 0 | |||
| 2 | |||
| 2 | |||
|- | |- | ||
| 3 | |||
| 0 | |||
| 1 | |||
| 1 | |||
| 3 | |||
| 3 | |||
|- | |||
| 4 | |||
| 1 | |||
| 0 | |||
| 0 | |||
| 4 | |||
| 4 | |||
|- | |||
| 5 | |||
| 1 | |||
| 0 | |||
| 1 | |||
| 5 | |||
| 5 | |||
|- | |||
| 6* | |||
| 1 | |||
| 1 | |||
| 0 | |||
| 6 | |||
| 6 | |||
|- | |- | ||
| 6 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | | 0 | ||
| 0 | | 0 | ||
|- | |- | ||
| 7 | |||
| 0 | |||
| 0 | |||
| 1 | | 1 | ||
| 1 | | 1 | ||
| 1 | |||
|- | |||
| 8 | |||
| 0 | |||
| 1 | |||
| 0 | |||
| 2 | |||
| 2 | |||
|} | |} | ||
*Não atingível. | |||
O diagrama de transição de estados do contador de 3 bits MOD-6 é mostrado na Figura 5. No diagrama de transição as linhas contínuas indicam a passagem pelos estados estáveis (000b 101b) e as linhas tracejadas indicam a passagem pelos estados temporários (110b). O estado (111b) embora possível não é atingível. | |||
[[Imagem:fig18_DIG222802.png|center|350px]] | |||
<center> | |||
Figura 5 - Diagrama de transição de estados de um contador MOD-6. | |||
</center> | |||
Para a construção de um contador módulo X menor que o módulo máximo, o procedimento deve seguir as etapas: | |||
*Determinar o menor número ''N'' de FF tal que <math>2^N \le X</math>. | |||
::Exemplo: MOD-12 <math>\rightarrow</math> N = 16. | |||
*Conectar a porta NAND nas entradas assíncronas <math>\overline{CLR}</math> de todos os FF. Se <math>2^N = X</math>, não é necessário conectar nada a entrada; | |||
*Conectar as saídas que estarão em ALTO na contagem X, na porta NAND. | |||
::Exemplo: 12 = 1100b D = 1 e C = 1, conectar D e C a porta NAND. | |||
==Decádicos== | |||
[[Imagem: | Os contadores de década (ou decádico) são contadores que possuem 10 estados distintos, não importando a sequência de contagem. Quando um contador decádico realiza a contagem em sequência binária crescente de 0000b a 1001b (0 a 9), ele é chamado de contador BCD. A Figura 6 mostra o CI 7490. | ||
[[Imagem:figura111_EDI018702.png|300px|center]] | |||
<center> | <center> | ||
Figura | Figura 6 - Circuito Integrado Contador 7490. | ||
</center> | </center> | ||
O circuito integrado TTL 7490 consiste num contador de década, divisor por 2 e por 5, com saídas BCD. Cada circuito integrado exige uma corrente de 32 mA e a máxima frequência de contagem é 18 MHz. A contagem ocorre nas transições negativas do sinal de ''clock''. Este circuito é encontrado em versões mais rápidas nas subfamílias TTLs correspondentes. [https://www.jameco.com/Jameco/Products/ProdDS/50690.pdf Datasheet 7490 - Contador Decádico] | |||
==Decrescente== | |||
[[Imagem: | Os contadores que contam progressivamente a partir do zero são denominados contadores crescentes (ou ascendentes). Já os contadores que contam do valor máximo até zero são chamados decrescentes (ou descendentes). A Figura 7 mostra a configuração para um contador decrescente construído com FF do tipo JK. A configuração é semelhante à do contador crescente, com a única diferença de cada FF é disparado pela saída '''Q\''' no lugar de '''Q'''. | ||
[[Imagem:fig19_DIG222802.png|center|500px]] | |||
<center> | <center> | ||
Figura | Figura 7 - Contador assíncrono decrescente. | ||
</center> | </center> | ||
A Figura 8 mostra o diagrama de tempo das saídas do contador, enquanto que a Tabela 3 mostra a contagem das transições do ''clock'' e os estados correspondentes ao contador. O diagrama de estados do contador decrescente é mostrado na Figura 9 (b), enquanto que o diagrama do contador crescente é mostrado na Figura 9 (a). Note que nos dois diagramas o contador passa por todos os estados. | |||
[[Imagem:fig20_DIG222802.png|center|350px]] | |||
<center> | |||
Figura 8 - Diagrama de tempo do contador assíncrono decrescente. | |||
</center> | |||
{| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
|+''' | |+'''Tabela 3 - Contador assíncrono decrescente MOD-8 (3 btis)''' | ||
|- | |- | ||
! style="background:# | ! style="background:#6A5ACD; color:white; width: 20px;" | Clock | ||
! style="background:# | ! style="background:#6A5ACD; color:white; width: 20px;" | C | ||
! style="background:# | ! style="background:#6A5ACD; color:white; width: 20px;" | B | ||
! style="background:#6A5ACD; color:white; width: 20px;" | A | |||
! style="background:#6A5ACD; color:white; width: 20px;" | Decimal | |||
! style="background:#6A5ACD; color:white; width: 20px;" | Estado | |||
|- | |- | ||
| 0 | | 0 | ||
| 0 | | 0 | ||
| | | 0 | ||
| 0 | |||
| 0 | |||
| 0 | |||
|- | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 7 | |||
| 1 | |||
|- | |||
| 2 | |||
| 1 | |||
| 1 | |||
| 0 | |||
| 6 | |||
| 2 | |||
|- | |||
| 3 | |||
| 1 | |||
| 0 | |||
| 1 | |||
| 5 | |||
| 3 | |||
|- | |||
| 4 | |||
| 1 | |||
| 0 | |||
| 0 | |||
| 4 | |||
| 4 | |||
|- | |||
| 5 | |||
| 0 | |||
| 1 | |||
| 1 | |||
| 3 | |||
| 5 | |||
|- | |- | ||
| 6 | |||
| 0 | | 0 | ||
| 1 | | 1 | ||
| 0 | | 0 | ||
| 2 | |||
| 6 | |||
|- | |- | ||
| 7 | |||
| 0 | |||
| 0 | |||
| 1 | |||
| 1 | | 1 | ||
| 7 | |||
|- | |||
| 8 | |||
| 0 | | 0 | ||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
|- | |||
| 9 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 7 | |||
| 1 | | 1 | ||
|- | |- | ||
| 10 | |||
| 1 | | 1 | ||
| 1 | | 1 | ||
| | | 0 | ||
| 6 | |||
| 2 | |||
|} | |} | ||
[[Imagem:fig21_DIG222802.png|center|450px]] | |||
<center> | |||
Figura 9 - Diagrama de transição de estados do contador MOD-8. | |||
</center> | |||
==Atrasos de Propagação== | |||
Em um contador assíncrono cada FF é disparado pela saída de um FF anterior. Essa característica traz como desvantagem o acumulo dos tempos de '''atraso de propagação'''. Isso pode ser visto na Figura 10. Ao passar por um FF, o sinal de ''clock'' sofre um atraso de propagação <math>t_{pd}</math> e esse efeito é somado até o último FF, gerando um atraso total de <math>N.t_{pd}</math>, onde N é o número de FF. | |||
[[Imagem: | [[Imagem:fig23_DIG222802.png|center|450px]] | ||
<center> | <center> | ||
Figura | Figura 10 - Contador assíncrono ascendente-descendente. | ||
</center> | </center> | ||
{ | Para que um contador assíncrono funcione de modo confiável é necessário que o atraso total de propagação seja menor que o período de ''clock'' usado: <math>T_{clk} \ge N.t_{pd}</math>, ou ainda, em termos de frequência máxima, que <math>f_{max}=\frac{1}{N.t_{pd}}</math>. | ||
=Exercício= | |||
[1] Complete o circuito abaixo para que funcione como contador '''assíncrono''' crescente. | |||
[[Imagem:fig78_DIG222802.png|center|600px]] | |||
{{collapse top|Contador Assíncrono de 3 bits com FF tipo D - ''falstad''}} | |||
Na página do falstad, copiar o código abaixo e colar em: Arquivo->Importar arquivo de texto... | |||
<pre> | |||
$ 1 0.000005 10.20027730826997 50 5 43 | |||
155 96 144 160 144 0 0 | |||
155 272 144 320 144 0 5 | |||
155 448 144 480 144 0 0 | |||
R 96 176 48 176 1 2 100 2.5 2.5 0 0.5 | |||
w 192 208 192 256 0 | |||
w 192 256 80 256 0 | |||
w 80 256 80 144 0 | |||
w 80 144 96 144 0 | |||
w 368 208 368 256 0 | |||
w 368 256 256 256 0 | |||
w 256 256 256 144 0 | |||
w 256 144 272 144 0 | |||
w 544 208 544 256 0 | |||
w 544 256 432 256 0 | |||
w 432 256 432 144 0 | |||
w 432 144 448 144 0 | |||
M 192 144 192 80 2 2.5 | |||
M 368 144 368 80 2 2.5 | |||
M 544 144 544 80 2 2.5 | |||
w 272 176 192 208 0 | |||
w 448 176 368 208 0 | |||
</pre> | |||
{{collapse bottom}} | |||
[2] Utilizando o mesmo circuito, faça as modificações necessárias para que funcione como contador '''assíncrono''' decrescente. | |||
=Referências= | |||
[1] Apostila do CURSO DE ELETRÔNICA DIGITAL. CEFET/SC: São José, 2011. | |||
Edição atual tal como às 15h46min de 1 de dezembro de 2020
1 Apresentação
Os contadores são circuitos que utilizam flip-flops e são aplicados, principalmente, em contagens, diversas, divisão de frequência, medição de frequência e tempo, divisão de formas de onda e conversão de analógico para digital. Estes circuitos sequenciais são divididos basicamente em duas categorias:
- Contadores assíncronos; e
- Contadores síncronos.
Basicamente a principal diferença entre eles é que o síncrono utiliza um sinal de clock comum a todos os flip-flops e o assíncrono possuí um sinal de clock que é dividido até o último flip-flops.
2 Contadores Assíncronos
Estes contadores também são conhecidos como seriais ou contadores por pulsação (ripple counter). Tal nome advém do fato dos flip-flops (FF) do contador não serem disparados diretamente pelo sinal de clock. Cada FF é disparado pela saída do FF anterior. Esta característica torna estes contadores limitados em termos de velocidade, pois o tempo de ativação (tempo de resposta) é dado aproximadamente pela soma dos tempos de atraso de propagação de cada FF.
2.1 Crescente
Um circuito típico de um contador assíncrono crescente construído com FF do tipo JK é mostrado na Figura 1. Os FF JK estão com ambas entradas J e K permanentemente em nível alto, estando configuradas portanto como FF tipo T. Cada FF é disparado pela saída do FF anterior. A Figura 2 mostra o diagrama de tempo para esse contador.

Figura 1 - Contador assíncrono crescente.
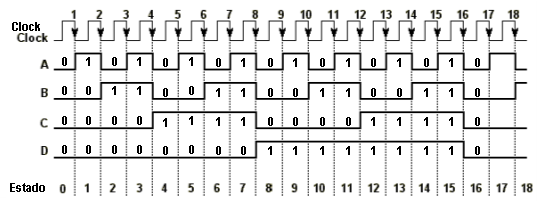
Figura 2 - Diagrama de tempo do contador assíncrono crescente.
| Clock | D | C | B | A | Decimal | Estado |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 2 | 2 |
| 3 | 0 | 0 | 1 | 1 | 3 | 3 |
| 4 | 0 | 1 | 0 | 0 | 4 | 4 |
| 5 | 0 | 1 | 0 | 1 | 5 | 5 |
| 6 | 0 | 1 | 1 | 0 | 6 | 6 |
| 7 | 0 | 1 | 1 | 1 | 7 | 7 |
| 8 | 1 | 0 | 0 | 0 | 8 | 8 |
| 9 | 1 | 0 | 0 | 1 | 9 | 9 |
| 10 | 1 | 0 | 1 | 0 | 10 | 10 |
| 11 | 1 | 0 | 1 | 1 | 11 | 11 |
| 12 | 1 | 1 | 0 | 0 | 12 | 12 |
| 13 | 1 | 1 | 0 | 1 | 13 | 13 |
| 14 | 1 | 1 | 1 | 0 | 14 | 14 |
| 15 | 1 | 1 | 1 | 1 | 15 | 15 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 1 | 1 | 1 |
| 18 | 0 | 0 | 1 | 0 | 2 | 2 |
O contador tem como conteúdo (estado interno) a contagem do número de transições negativas do clock, de forma que quando ocorre uma transição o conteúdo é incrementado de uma unidade. O conteúdo do contador é dado pelo número binário DCBA, onde A é o bit LSB (bit menos significativo) e D é o bit MSB (bit mais significativo). O modulo (MOD) de um contador é o seu número de estados distintos, portanto, o módulo de um contador com N FF pode ser no máximo o número de possíveis saídas (). A Tabela mostra os estados de contagem de um contador assíncrono com 4 FF (4 bits). Podemos perceber que após 16 transições de clock o contador reinicia a contagem. Por isso, este contador é de MOD-16, ou seja, tem 16 estados distintos (0000b até 1111b). Nos contadores assíncronos, a frequência do clock é dividida por 2 em cada FF, ou seja: na saída A temos clock/2, e na saída D temos clock/16. Portanto, os contadores assíncronos são divisores de frequência e no último FF a frequência de clock é dividida pelo módulo do contador.
| Circuito do Contador Assíncrono de 3 bits - falstad |
|---|
|
Na página do falstad, copiar o código abaixo e colar em: Arquivo->Importar arquivo de texto... $ 1 0.000005 10.20027730826997 50 5 43 156 96 96 176 96 0 5 156 256 96 272 96 0 5 156 416 96 448 96 0 0 L 96 96 64 96 2 1 false 5 0 L 96 160 64 160 2 1 false 5 0 L 256 96 240 96 2 1 false 5 0 L 256 160 240 160 2 1 false 5 0 L 416 96 400 96 2 1 false 5 0 L 416 160 400 160 2 1 false 5 0 M 192 96 192 32 2 2.5 M 352 96 352 32 2 2.5 M 512 96 512 32 2 2.5 R 96 128 48 128 1 2 100 2.5 2.5 0 0.5 w 256 128 192 96 0 w 416 128 352 96 0 403 0 240 544 288 0 12_64_0_4099_5_0.00009765625_0_2_12_3 403 0 288 544 320 0 9_64_0_4098_5_0.1_0_1 403 0 336 544 368 0 10_64_0_4098_5_0.1_0_1 403 0 384 544 416 0 11_64_0_4098_5_0.1_0_1 |
2.2 Contadores de Módulo
Para obter um contador com módulo menor do que é necessário adicionar um circuito decodificador para reiniciar a contagem antes de chegar ao valor máximo (ou mínimo). A Figura 3 mostra um contador MOD-6. Se não houvesse a porta NAND ligada nas entradas CLR dos FF o módulo do contador seria 8. A sequência de estados do contador MOD-6 é mostrada nas Figura 4 e Tabela 2. Note que na transição do 6º clock o estado do contador passa temporariamente pelo estado (110b), o qual faz com que a saída da porta NAND passe para o estado BAIXO, causando o CLR nos FF, e consequentemente levando o contador para o estado (000b).
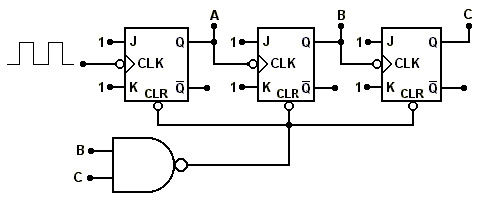
Figura 3 - Contador assíncrono com módulo < .
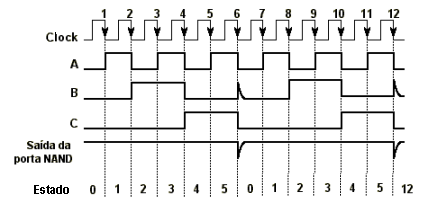
Figura 4 - Diagrama de tempo do contador com módulo < .
| Clock | C | B | A | Decimal | Estado |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 2 | 0 | 1 | 0 | 2 | 2 |
| 3 | 0 | 1 | 1 | 3 | 3 |
| 4 | 1 | 0 | 0 | 4 | 4 |
| 5 | 1 | 0 | 1 | 5 | 5 |
| 6* | 1 | 1 | 0 | 6 | 6 |
| 6 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 1 | 1 | 1 |
| 8 | 0 | 1 | 0 | 2 | 2 |
*Não atingível.
O diagrama de transição de estados do contador de 3 bits MOD-6 é mostrado na Figura 5. No diagrama de transição as linhas contínuas indicam a passagem pelos estados estáveis (000b 101b) e as linhas tracejadas indicam a passagem pelos estados temporários (110b). O estado (111b) embora possível não é atingível.
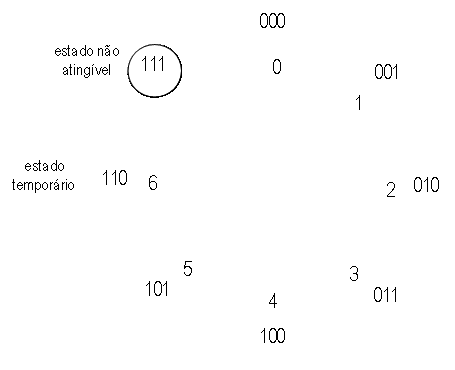
Figura 5 - Diagrama de transição de estados de um contador MOD-6.
Para a construção de um contador módulo X menor que o módulo máximo, o procedimento deve seguir as etapas:
- Determinar o menor número N de FF tal que .
- Exemplo: MOD-12 N = 16.
- Conectar a porta NAND nas entradas assíncronas de todos os FF. Se , não é necessário conectar nada a entrada;
- Conectar as saídas que estarão em ALTO na contagem X, na porta NAND.
- Exemplo: 12 = 1100b D = 1 e C = 1, conectar D e C a porta NAND.
2.3 Decádicos
Os contadores de década (ou decádico) são contadores que possuem 10 estados distintos, não importando a sequência de contagem. Quando um contador decádico realiza a contagem em sequência binária crescente de 0000b a 1001b (0 a 9), ele é chamado de contador BCD. A Figura 6 mostra o CI 7490.

Figura 6 - Circuito Integrado Contador 7490.
O circuito integrado TTL 7490 consiste num contador de década, divisor por 2 e por 5, com saídas BCD. Cada circuito integrado exige uma corrente de 32 mA e a máxima frequência de contagem é 18 MHz. A contagem ocorre nas transições negativas do sinal de clock. Este circuito é encontrado em versões mais rápidas nas subfamílias TTLs correspondentes. Datasheet 7490 - Contador Decádico
2.4 Decrescente
Os contadores que contam progressivamente a partir do zero são denominados contadores crescentes (ou ascendentes). Já os contadores que contam do valor máximo até zero são chamados decrescentes (ou descendentes). A Figura 7 mostra a configuração para um contador decrescente construído com FF do tipo JK. A configuração é semelhante à do contador crescente, com a única diferença de cada FF é disparado pela saída Q\ no lugar de Q.
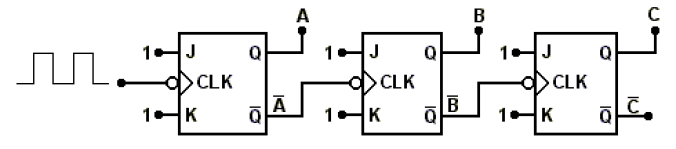
Figura 7 - Contador assíncrono decrescente.
A Figura 8 mostra o diagrama de tempo das saídas do contador, enquanto que a Tabela 3 mostra a contagem das transições do clock e os estados correspondentes ao contador. O diagrama de estados do contador decrescente é mostrado na Figura 9 (b), enquanto que o diagrama do contador crescente é mostrado na Figura 9 (a). Note que nos dois diagramas o contador passa por todos os estados.
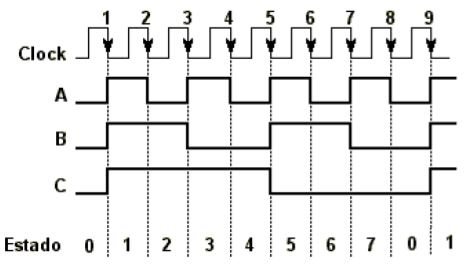
Figura 8 - Diagrama de tempo do contador assíncrono decrescente.
| Clock | C | B | A | Decimal | Estado |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 7 | 1 |
| 2 | 1 | 1 | 0 | 6 | 2 |
| 3 | 1 | 0 | 1 | 5 | 3 |
| 4 | 1 | 0 | 0 | 4 | 4 |
| 5 | 0 | 1 | 1 | 3 | 5 |
| 6 | 0 | 1 | 0 | 2 | 6 |
| 7 | 0 | 0 | 1 | 1 | 7 |
| 8 | 0 | 0 | 0 | 0 | 0 |
| 9 | 1 | 1 | 1 | 7 | 1 |
| 10 | 1 | 1 | 0 | 6 | 2 |
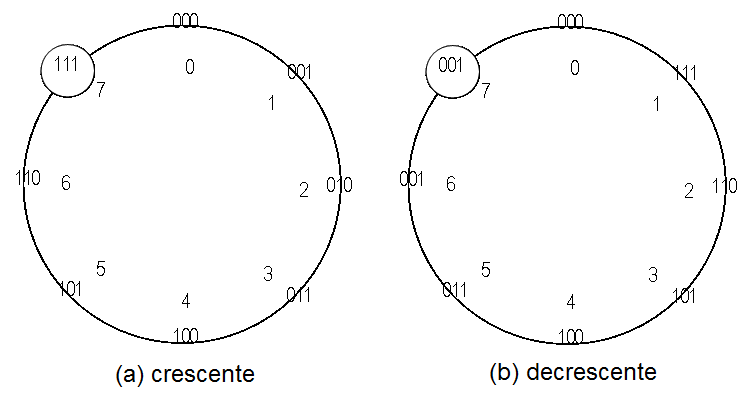
Figura 9 - Diagrama de transição de estados do contador MOD-8.
2.5 Atrasos de Propagação
Em um contador assíncrono cada FF é disparado pela saída de um FF anterior. Essa característica traz como desvantagem o acumulo dos tempos de atraso de propagação. Isso pode ser visto na Figura 10. Ao passar por um FF, o sinal de clock sofre um atraso de propagação e esse efeito é somado até o último FF, gerando um atraso total de , onde N é o número de FF.
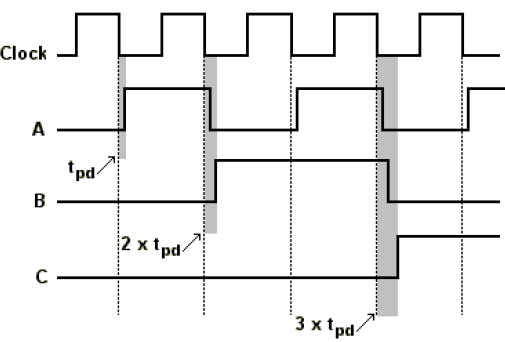
Figura 10 - Contador assíncrono ascendente-descendente.
Para que um contador assíncrono funcione de modo confiável é necessário que o atraso total de propagação seja menor que o período de clock usado: , ou ainda, em termos de frequência máxima, que .
3 Exercício
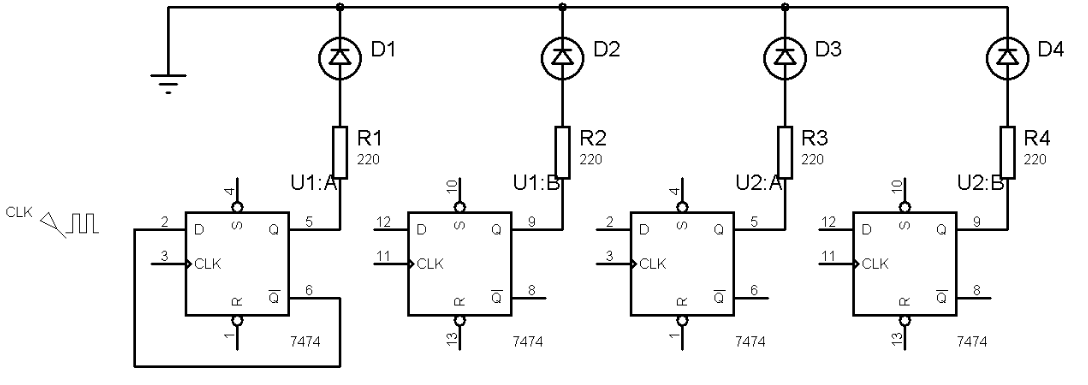
[1] Complete o circuito abaixo para que funcione como contador assíncrono crescente.
| Contador Assíncrono de 3 bits com FF tipo D - falstad |
|---|
|
Na página do falstad, copiar o código abaixo e colar em: Arquivo->Importar arquivo de texto... $ 1 0.000005 10.20027730826997 50 5 43 155 96 144 160 144 0 0 155 272 144 320 144 0 5 155 448 144 480 144 0 0 R 96 176 48 176 1 2 100 2.5 2.5 0 0.5 w 192 208 192 256 0 w 192 256 80 256 0 w 80 256 80 144 0 w 80 144 96 144 0 w 368 208 368 256 0 w 368 256 256 256 0 w 256 256 256 144 0 w 256 144 272 144 0 w 544 208 544 256 0 w 544 256 432 256 0 w 432 256 432 144 0 w 432 144 448 144 0 M 192 144 192 80 2 2.5 M 368 144 368 80 2 2.5 M 544 144 544 80 2 2.5 w 272 176 192 208 0 w 448 176 368 208 0 |
[2] Utilizando o mesmo circuito, faça as modificações necessárias para que funcione como contador assíncrono decrescente.
4 Referências
[1] Apostila do CURSO DE ELETRÔNICA DIGITAL. CEFET/SC: São José, 2011.