CEL18702 2017 1 AULA08

1 Análise Nodal

Na aula anterior, de conteúdo, estudamos circuitos resistivos utilizando análise nodal. Agora vamos transformar as resistências em condutâncias e resolver esses mesmos circuitos da mesma forma de como se fossem resistências, retirando a questão das frações das equações.

Nota: Um circuito com três nós terá duas tensões incógnitas e duas equações; um circuito com dez nós terá nove tensões desconhecidas e nove equações; um circuito com N nós terá N-1 tensões incógnitas e N-1 equações.

2 Condutância

Vamos abrir um parênteses para falar sobre condutância. A ideia é que os circuitos fiquem em "termos" de multiplicação e não de divisão. A Figura 1 mostra um exemplo que permite escrever as equações de nós por inspeção direta em função da tensão dos nós.

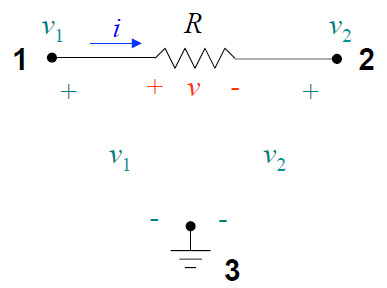
Figura 1 - Exemplos de circuito resistivo x condutivo.

$V=V_1-V_2$

$i=\frac{V}{R}=\frac{V_1-V_2}{R}$ ou $i=\frac{V}{R}=G(V_1-V_2)$

Fórmula matemática da condutância

Para calcular a condutância de um determinado condutor, temos que saber o valor da sua resistência. Assim, e sabendo que a condutância é o inverso da resistência, chegamos à seguinte fórmula:

$G=\frac{1}{R}$

Se tivermos por exemplo, um condutor em que a resistência seja igual a 10Ω, substituímos o R de resistência por 10Ω e obtemos o seguinte cálculo:

Então

$G=\frac{1}{R}=\frac{1}{10}=0,1S(siemens)$

Logo com este cálculo concluímos que um condutor com uma resistência de 10Ω, tem uma condutância de 0,1 siemens.

2.1 Exemplo 1

Tomemos esse exemplo para o qual faremos a mesma análise do dos exercícios anteriores. O exemplo que se segue é de um circuito com um único par de nós possuindo também fontes dependentes:

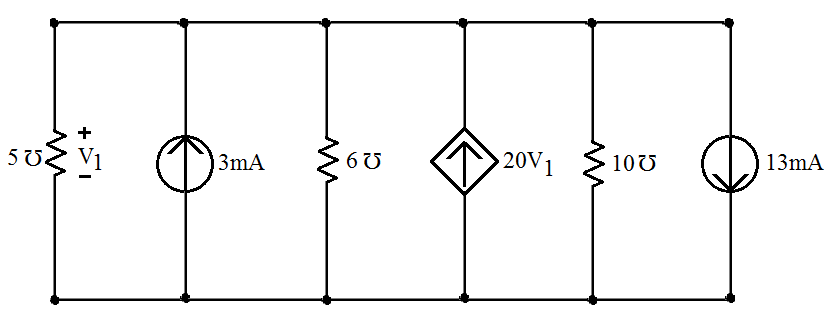
Figura 1 - Aplicação da lei dos nós a um circuito com fontes dependentes.

Como se pode verificar, a tensão $V_1$ aplicada sobre a condutância de 5 está também aplicada sobre todos os elementos do circuito. Considerando que a corrente sobre as condutâncias estão com a seta dirigida para o nó inferior e aplicamos a lei dos nós.

$5V_1-0,003+6V_1-20V_1+10V_1+0,013=0$

$1V_1=-0,003-0,013\to V_1=-0,01V$

Podemos agora determinar as correntes sobre as condutâncias assim como a potência fornecida ou consumida por cada um dos elementos.

Na condutância 5

$i_5=5V_1=-0,05A$

$P_5=5V_1^2=5(-0,01{)}^2=5.10^{-4}W$

Na condutância 6

$i_6=6V_1=-0,06A$

$P_6=6V_1^2=5(-0,01{)}^2=6.10^{-4}W$

Na condutância 10

$i_{10}=10V_1=-0,1A$

$P_{10}=10V_1^2=10(-0,01{)}^2=1.10^{-3}W$

Potência fornecida pela fonte de 3mA

$P_{f3ma}=0,003V_1=-0,3.10^{-4}W;P_a=0,3.10^{-4}W$

Potência fornecida pela fonte de 13mA

$P_{f13ma}=-0,013V_1=-1,3.10^{-4}W$

Potência fornecida pela fonte dependente

$P_{f20Vx}=20V_1.V_1=20V_1^2=20(-0,01{)}^2=20.10^{-4}W$

Por último, fazemos o balanço das potências

$\sum _{}^{}{P}_f=1,3.10^{-4}+20.10^{-4}=21,3.10^{-4}W$

$\sum _{}^{}{P}_a=5.10^{-4}+6.10^{-4}+0,3.10^{-4}=21,3.10^{-4}W$

3 Exemplo 2

Utilizando análise nodal encontre as tensões nos nós do circuito e encontre as correntes em todos os resistores.

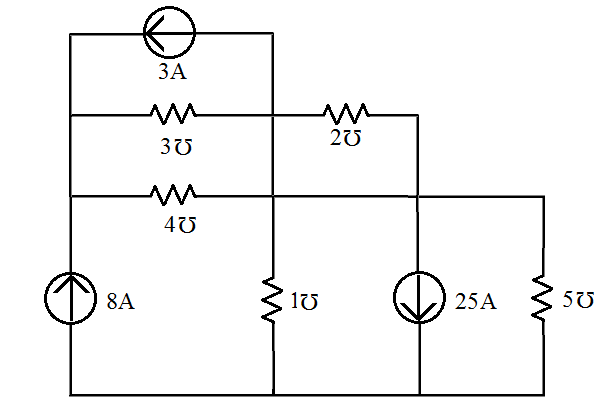
Resolvendo o Circuito

Definindo os nós do circuito ($V_{1}e{V}_2$).

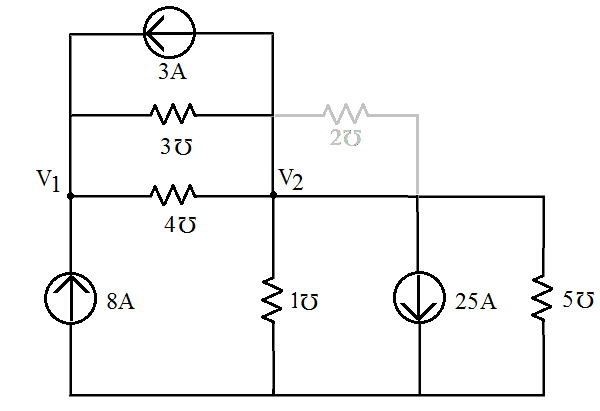
Percebe-se que a condutância de 2 está curtocircuitada, portanto, não será considerada no sistema.

Outra definição importante é que devemos atribuir o sinal da corrente que chega e que sai do nó. Podendo ser negativas as correntes que chegam no nó e positivas as correntes que saem do nó. Lembrando, não há nenhum problema em arbitrar essas corrente de forma contrária, tendo como resultados os valores com troca de sinal.

Resposta
V1=-1,26V; V2=-2,83V;

4 Exercícios

[1] Ache as tensões dos nós $V_{1}e{V}_2$

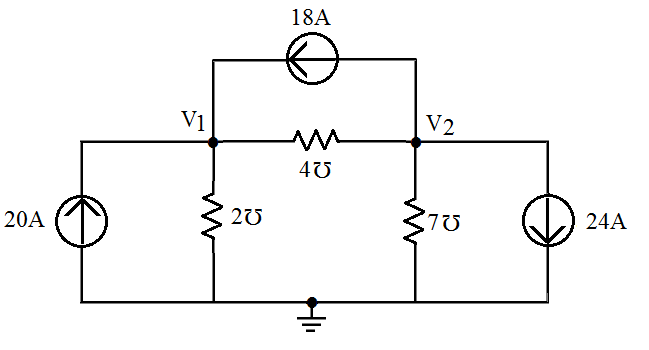
Solução
Nó 1 $(2+4)v_1-4v_2=20+18$ $6v_1-4v_2=38$ Nó 2 $(4+7)v_2-4v_1=-18-24$ $-4v_1+11v_2=-42$ Resultado $V_1=5V$ $V_2=-2V$

[2] Ache as tensões dos nós $V_1,V_{2}e{V}_3$

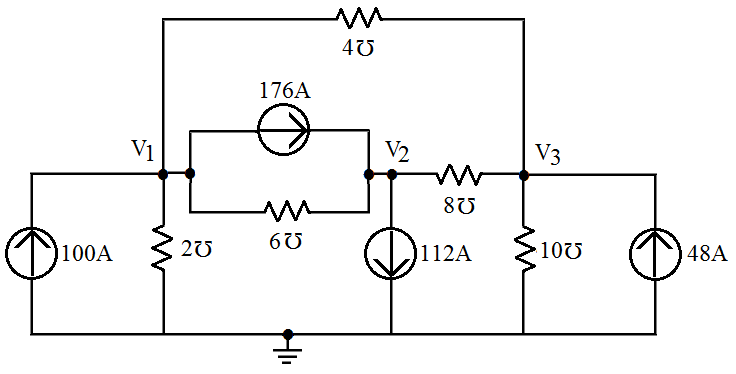
Solução
Resultado $V_1=-2$ $V_2=4V$ $V_2=6V$

5 Referências

[1] http://www.decom.fee.unicamp.br/~baldini/EA513/Cap4.pdf

---