|
|
| (78 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) |
| Linha 1: |
Linha 1: |
| − | =Análise de Circuitos Elétricos de CC em Regime Permanente= | + | =Técnicas Utilizadas na Análise de Circuitos= |
| | | | |
| | + | ==Análise de Malhas== |
| | | | |
| − | ==Leis de Kirchhoff==
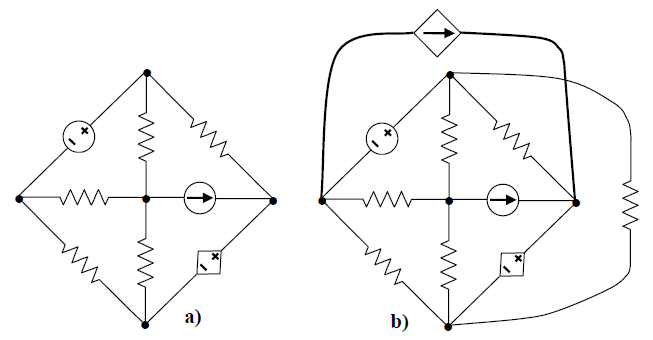
| + | O método de análise das malhas só é aplicado às redes planares. Se for possível desenhar o |
| | + | diagrama de um circuito numa superfície plana, sem que haja cruzamento dos ramos, então o circuito é |
| | + | dito planar. Na Figura 1 temos um exemplo de rede planar e não planar. |
| | | | |
| − | Inicialmente, será apresentada uma discussão sobre polaridade e tensão nos elementos componentes de um circuito elétrico. Desta forma, será possível calcular a tensão nos extremos do trecho de um circuito.
| + | [[Imagem:fig28_CEL18702.png|center|500px]] |
| − | Para geradores e receptores ideais, independentemente do sentido da corrente elétrica, o traço menor representa o polo negativo e o traço maior corresponde ao polo positivo, conforme a Figura 1.
| |
| − | | |
| − | [[Imagem:fig16_CEL18702.png|center]] | |
| | <center> | | <center> |
| − | Figura 1 - Representação da polaridade de um gerador ou um receptor ideal. | + | Figura 1 - Rede planar (a) e Rede não planar (b). |
| | </center> | | </center> |
| | | | |
| − | O polo B tem potencial elétrico maior que o polo A, ou seja, no sentido da seta da Figura 1, a tensão é positiva. Logo, tem-se: | + | Um circuito é uma rede que contém pelo menos um caminho fechado por onde possa fluir |
| | + | corrente. O nome oficial para esse caminho é laço. Assim, se iniciarmos por um determinado nó e |
| | + | traçarmos pela rede uma linha fechada contínua, passando uma vez em cada nó e terminando no nó de |
| | + | partida, este caminho é um laço. A malha é uma propriedade de circuitos planares e é definida como |
| | + | sendo um laço que não contém nenhum outro por dentro. |
| | | | |
| | + | A técnica de análise de malhas envolve o conceito de corrente de malha que definiremos como |
| | + | sendo a corrente que flui apenas no perímetro de uma malha. |
| | + | Vamos utilizar o exemplo da Figura 2 para melhor entendimento do método. |
| | + | |
| | + | [[Imagem:fig26_CEL18702.png|center|400px]] |
| | <center> | | <center> |
| − | <math>V_B - V_A = +E\,</math>
| + | Figura 2 - Exemplo de aplicação do método de malhas. |
| − | | |
| − | <math>V_A-V_B = -E\,</math>
| |
| | </center> | | </center> |
| | | | |
| | + | ;Solução: |
| | | | |
| − | Para os resistores, a polaridade é dada pelo sentido da corrente: o polo positivo é o da entrada da corrente, e negativo é o da saída, segundo a Figura 2.
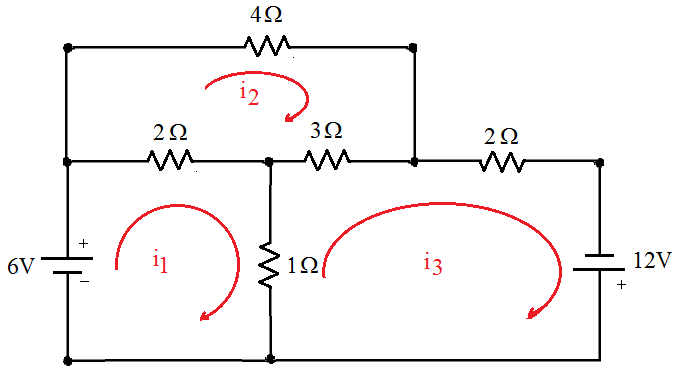
| + | #Arbitramos as correntes de malhas dando a designação de <math>i_1\,</math> para a malha 1, <math>i_2\,</math> para a malha 2 e assim por diante; |
| | + | #O sentido arbitrado para as correntes de malha pode ser qualquer um, mas para facilitar a obtenção das equações adotamos sempre o sentido horário; |
| | + | #Escreve-se as equações de malha em termos das tensões utilizando a lei de Ohm <math>V=RI\,</math> |
| | + | #Simplifica-se as equações e resolve-se o sistema obtido. |
| | | | |
| − | [[Imagem:fig17_CEL18702.png|center]]
| + | ;Malha 1: |
| − | <center> | + | <math> |
| − | Figura 2 - Representação da polaridade da tensão em um resistor.
| + | -6+2(i_1-i_2)+1(i_1-i_3)=0 \quad \to \quad -6+2i_1-2i_2+1i_1-2i_3=0 |
| − | </center> | + | </math> |
| | | | |
| − | O polo A tem potencial elétrico maior que o polo B, ou seja, a tensão é positiva no sentido oposto ao de circulação da corrente. Logo, tem-se:
| + | ;Malha 2: |
| | + | <math> |
| | + | 4i_2+3(i_2-i_3)+2(i_2-i_1)=0 \quad \to \quad 4i_2+3i_2-3i_3+2i_2-2i_1=0 |
| | + | </math> |
| | | | |
| − | <center>
| + | ;Malha 3: |
| − | <math>V_A - V_B = +R.I\,</math> | + | <math> |
| | + | -12+2i_3+1(i_3-i_1)+3(i_3-i_2)=0 \quad \to \quad -12+2i_3+1i_3-1i_1+3i_3-3i_2=0 |
| | + | </math> |
| | | | |
| − | <math>V_B - V_A = -R.I\,</math>
| + | Arrumando... |
| − | </center>
| |
| | | | |
| − | Portanto, para o cálculo da tensão entre os extremos de um trecho de circuito, deve-se:
| + | <math>3i_1-2i_2-i_3=6\,</math> |
| | | | |
| − | *Verificar o sentido de circulação da corrente;
| + | <math>-2i_1+9i_2-3i_3=0\,</math> |
| − | *Marcar as polaridades das tensões de acordo com tal sentido;
| |
| − | *Efetuar o somatório das mesmas.
| |
| | | | |
| − | Na Figura 3, tem-se um exemplo básico.
| + | <math>-i_1-3i_2+6i_3=12\,</math> |
| | | | |
| | | | |
| − | [[Imagem:fig18_CEL18702.png|center]]
| + | <math> |
| − | <center> | + | \Delta=\begin{vmatrix} 3 & -2 & -1 \\ -2 & 9 & -3 \\ -1 & -3 & 6 \end{vmatrix}\,.\,\begin{vmatrix} 6 \\ 0 \\ 12 \end{vmatrix} |
| − | Figura 3 - Trecho do circuito.
| + | </math> |
| − | </center> | |
| | | | |
| − | Seguindo os passos anteriormente descritos, chega-se à Figura 4.
| |
| | | | |
| | + | <math> |
| | + | det \Delta=\begin{vmatrix} 3 & -2 & -1 \\ -2 & 9 & -3 \\ -1 & -3 & 6 \end{vmatrix}\,=\, 90 |
| | + | </math> |
| | | | |
| − | [[Imagem:fig19_CEL18702.png|center]]
| |
| − | <center>
| |
| − | Figura 4 - Trecho do circuito com marcação das tensões.
| |
| − | </center>
| |
| − |
| |
| − | Assim, a diferença potencial entre A e B é:
| |
| | | | |
| − | <center>
| |
| | <math> | | <math> |
| − | V_A - V_B = +r_1.I-E_1+R.I+E_2+r_2.I\,
| + | det \Delta\,i_1=\begin{vmatrix} 6 & -2 & -1 \\ 0 & 9 & -3 \\ 12 & -3 & 6 \end{vmatrix}\,= 450 |
| | </math> | | </math> |
| − | </center>
| |
| | | | |
| − | ==Lei dos Nós==
| |
| | | | |
| − | Em um circuito elétrico, denomina-se nó um ponto comum a três ou mais condutores. Veja Figura 5.
| + | <math> |
| − | | + | det \Delta\,i_2=\begin{vmatrix} 3 & 6 & -1 \\ -2 & 0 & -3 \\ -1 & 12 & 6 \end{vmatrix}\,= 222 |
| − | [[Imagem:fig20_CEL18702.png|center]]
| + | </math> |
| − | <center> | |
| − | Figura 5 - Nó de um circuito.
| |
| − | </center> | |
| | | | |
| − | Assim, pode-se enunciar a primeira lei de Kirchhoff: “A soma das intensidades das correntes que chegam a um nó é igual à soma da intensidade das correntes que saem do mesmo”.
| |
| − | No exemplo da Figura 5, tem-se:
| |
| | | | |
| − | <center>
| |
| | <math> | | <math> |
| − | I_1=I_2+I_3\,
| + | det \Delta\,i_3=\begin{vmatrix} 3 & -2 & 6 \\ -2 & 9 & 0 \\ -1 & -3 & 12 \end{vmatrix}\,= 336 |
| | </math> | | </math> |
| − | </center>
| |
| | | | |
| − | ==Lei das Malhas==
| |
| | | | |
| − | Em um circuito elétrico, denomina-se malha um conjunto de elementos de circuito constituindo um percurso fechado, como é mostrado na Figura 6.
| + | <math> |
| | + | i_1= \frac{\Delta\,i_1}{\Delta}\, \qquad i_1=\frac{450}{90}=5A |
| | + | </math> |
| | | | |
| | | | |
| − | [[Imagem:fig21_CEL18702.png|center]]
| + | <math> |
| − | <center> | + | i_2= \frac{\Delta\,i_2}{\Delta}\, \qquad i_2=\frac{222}{90}=2,47A |
| − | Figura 6 - Malha de um circuito.
| + | </math> |
| − | </center> | |
| − | | |
| | | | |
| − | Assim, pode-se enunciar a segunda lei de Kirchhoff: “Percorrendo uma malha em um certo sentido, partindo e chegando ao mesmo ponto, a soma algébrica das tensões é nula”.
| |
| − | No exemplo da Figura 6, tem-se a malha ABCD. Partindo-se do ponto A, adotando-se o sentido horário e retornando ao mesmo ponto, pode-se escrever:
| |
| | | | |
| − | <center>
| |
| | <math> | | <math> |
| − | R_2.I_2+E_2+r_2.I_2+R_1.I_2+r_1.I_1-E_1=0\,
| + | i_3= \frac{\Delta\,i_3}{\Delta}\, \qquad i_3=\frac{366}{90}=4,07A |
| | </math> | | </math> |
| − | </center>
| |
| | | | |
| | ==Exercício de Fixação== | | ==Exercício de Fixação== |
| | | | |
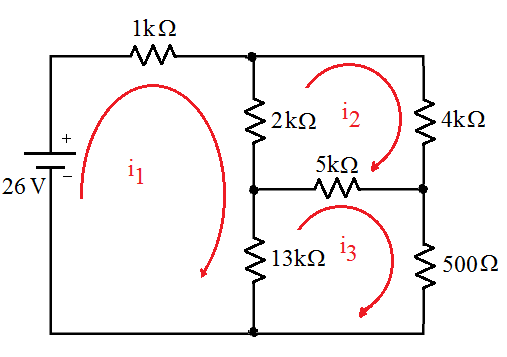
| − | [[Imagem:fig25_CEL18702.png|center]] | + | Determine o valor de todas as '''correntes''' no circuito (mesmo circuito redesenhado) e a queda de '''tensão''' em todos os resistores: |
| | + | |
| | + | [[Imagem:fig30_CEL18702.png|center]] |
| | + | |
| | | | |
| | {{collapse top|Solução}} | | {{collapse top|Solução}} |
| | | | |
| − | A primeira coisa a se fazer é atribuirmos um sentido de corrente. Depois, atribuir um sentido para cada malha, que também pode ser aleatório. No caso do circuito acima, preferimos utilizar o sentido horário.
| + | ;Malha 1 |
| − | | |
| − | ;Aplicando o lei do nós: | |
| | | | |
| | <math> | | <math> |
| − | i_1=i_2+i_6\,\qquad (I) | + | -26+1ki_1+2k(i_1-i_2)+13k(i_1-i_3)=0\, \to \, -26+1ki_1+2ki_1-2ki_2+13ki_2-13ki_3=0\, \to \, 16ki_1-2ki_2-13ki_3=26 |
| | </math> | | </math> |
| | | | |
| − | <math>
| + | ;Malha 2 |
| − | i_2=i_3+i_4\,\qquad (II)
| |
| − | </math>
| |
| | | | |
| | <math> | | <math> |
| − | i_5=i_3+i_4\,\qquad (III)
| + | 4ki_2+5k(i_2-i_3)+2k(i_2-i_1)=0\, \to \, 4ki_2+5ki_2-5ki_3+2ki_2-2ki_1=0 \, \to \, -2ki_1+11ki_2-5ki_3=0 |
| | </math> | | </math> |
| | | | |
| − | ;Malha A | + | ;Malha 3 |
| | | | |
| | <math> | | <math> |
| − | -10 + 1.i_1 -20 + 2i_1 = 0\,\qquad 3i_1=30 \qquad i_1=\frac{30}{3} \qquad i_1=10A | + | 5k(i_3-i_2)+0.5ki_3+13k(i_3-i_1)=0\, \to \, 5ki_3-5ki_2+0.5ki_3+13ki_3-13ki_1=0\, \to \, -13ki_1 -5ki_2+18.5ki_3=0 |
| | </math> | | </math> |
| | | | |
| − | ;Malha B
| |
| | | | |
| − | <math>
| + | ;Organizando |
| − | +20 + 2.i_2 +10 + 1i_5 = 0\,\qquad 2i_2+1i_5=-30
| |
| − | </math>
| |
| | | | |
| − | ;Malha C
| + | <math>16000i_1-2000i_2-13000i_3=26\,</math> |
| | | | |
| − | <math> | + | <math>-2000i_1+11000i_2-5000i_3=0\,</math> |
| − | -10 + 1.i_3 -20 + 2i_3 = 0\,\qquad 3i_3=30 \qquad i_3=\frac{30}{3} \qquad i_3=10A | |
| − | </math> | |
| | | | |
| − | Substituindo os valores de <math>i_1 e\, i_3</math>em I, II e III:
| + | <math>-13000i_1 -5000i_2+18500i_3=0\,</math> |
| | | | |
| − | <math>
| |
| − | i_1=i_2+i_6 \,\qquad 10=i_2+i_6 \qquad i_2+i_6=10
| |
| − | </math>
| |
| | | | |
| − | <math>
| + | ;Resolvendo por Cramer: |
| − | i_2=i_3+i_4 \,\qquad i_2=10+i_4 \qquad i_2-i_4=10
| |
| − | </math>
| |
| | | | |
| | <math> | | <math> |
| − | i_5=i_3+i_4 \,\qquad i_5=10+i_4 \qquad i_5-i_4=10
| + | \Delta=\begin{vmatrix} 16000 & -2000 & -13000 \\ -2000 & 11000 & -5000 \\ -13000 & -5000 & 18500 \end{vmatrix}\,.\,\begin{vmatrix} 26 \\ 0 \\ 0 \end{vmatrix} |
| | </math> | | </math> |
| | | | |
| | | | |
| − | Mais IV, forma-se um sistema de quatro equações e quatro incógnitas.
| + | ;Resultado confirmado (matlab/calc): |
| − | | |
| − | <math>i_2+i_6=10\,</math>
| |
| − | | |
| − | <math>i_2-i_4=10\,</math>
| |
| | | | |
| − | <math>i_5-i_4=10\,</math> | + | <math>\Delta = 663000000000\,</math> |
| | | | |
| − | <math>2i_2+i_5=-30\,</math>
| |
| | | | |
| | + | <math>\Delta i_1 = 4641000000\,</math> |
| | | | |
| − | Isolando...
| + | <math>\Delta i_2 = 2652000000\,</math> |
| | | | |
| − | <math>i_4=i_2-10\,</math> | + | <math>\Delta i_3 = 3978000000\,</math> |
| | | | |
| − | Substituindo...
| + | <math>i_1 = 0,007 A\,</math> |
| | | | |
| − | <math> | + | <math>i_2 = 0,004 A\,</math> |
| − | i_5-(i_2-10)=10\, \qquad i_5-i_2+10=10 \qquad i_5-i_2=0 \qquad i_5=i_2
| |
| − | </math> | |
| | | | |
| − | <math> | + | <math>i_3 = 0,006 A\,</math> |
| − | 2i_2+i_2=-30\, \qquad 3i_2=-30 \qquad i_2=-\frac{30}{3} \qquad i_2=-10A
| |
| − | </math> | |
| | | | |
| − | Assim...
| + | <math>V_{1k} = 7 V\,</math> |
| | | | |
| − | <math> | + | <math>V_{2k} = 6 V\,</math> |
| − | i_5=i_2\, \qquad i_5=-10A
| |
| − | </math> | |
| | | | |
| − | <math> | + | <math>V_{4k} = 16 V\,</math> |
| − | i_4=i_2-10\, \qquad i_4=-10-10 \qquad i_4=-10A
| |
| − | </math> | |
| | | | |
| − | Por último...
| + | <math>V_{5k} = -10 V\,</math> |
| | | | |
| − | <math> | + | <math>V_{13k} = 13 V\,</math> |
| − | i_2+i_6=10\, \qquad -10+i_6=10 \qquad i_6=10+10 \qquad i_6=20A
| |
| − | </math> | |
| | | | |
| − | Como o valor das correntes <math> i_2, i_4 e\, i_5</math> são negativos, isto significa que foram atribuídos sentidos contrários no exercício.
| + | <math>V_{500} = 3 V\,</math> |
| | | | |
| | | | |
| Linha 214: |
Linha 182: |
| | ----- | | ----- |
| | {| border="1" cellpadding="5" cellspacing="0" | | {| border="1" cellpadding="5" cellspacing="0" |
| − | ! style="background: #ffd700;" | [[CEL18702_AULA03 | << ]] | + | ! style="background: #ffd700;" | [[CEL18702_AULA04 | << ]] |
| | ! style="background: #faebd7;" | [[CEL18702 | <> ]] | | ! style="background: #faebd7;" | [[CEL18702 | <> ]] |
| − | ! style="background: #ffd700;" | [[CEL18702 | >> ]] | + | ! style="background: #ffd700;" | [[CEL18702_AULA06 | >> ]] |
| | |} | | |} |
Técnicas Utilizadas na Análise de Circuitos
Análise de Malhas
O método de análise das malhas só é aplicado às redes planares. Se for possível desenhar o
diagrama de um circuito numa superfície plana, sem que haja cruzamento dos ramos, então o circuito é
dito planar. Na Figura 1 temos um exemplo de rede planar e não planar.
Figura 1 - Rede planar (a) e Rede não planar (b).
Um circuito é uma rede que contém pelo menos um caminho fechado por onde possa fluir
corrente. O nome oficial para esse caminho é laço. Assim, se iniciarmos por um determinado nó e
traçarmos pela rede uma linha fechada contínua, passando uma vez em cada nó e terminando no nó de
partida, este caminho é um laço. A malha é uma propriedade de circuitos planares e é definida como
sendo um laço que não contém nenhum outro por dentro.
A técnica de análise de malhas envolve o conceito de corrente de malha que definiremos como
sendo a corrente que flui apenas no perímetro de uma malha.
Vamos utilizar o exemplo da Figura 2 para melhor entendimento do método.
Figura 2 - Exemplo de aplicação do método de malhas.
- Solução
- Arbitramos as correntes de malhas dando a designação de
 para a malha 1,
para a malha 1,  para a malha 2 e assim por diante;
para a malha 2 e assim por diante;
- O sentido arbitrado para as correntes de malha pode ser qualquer um, mas para facilitar a obtenção das equações adotamos sempre o sentido horário;
- Escreve-se as equações de malha em termos das tensões utilizando a lei de Ohm

- Simplifica-se as equações e resolve-se o sistema obtido.
- Malha 1

- Malha 2

- Malha 3

Arrumando...











Exercício de Fixação
Determine o valor de todas as correntes no circuito (mesmo circuito redesenhado) e a queda de tensão em todos os resistores:
| Solução
|
- Malha 1

- Malha 2

- Malha 3

- Organizando



- Resolvendo por Cramer

- Resultado confirmado (matlab/calc)













|
Referências
[1] http://www.feng.pucrs.br/~virgilio/Circuitos_Eletricos_I/Capitulo3_ckt1.pdf
[2] http://www3.fsa.br/localuser/Eletronica/mario.garcia/Circuitos%20el%C3%A9tricos%20I/Determinantes.PDF