Multiplicação Binária
A multiplicação binária é semelhante a multiplicação decimal, considerando que a base de representação é 2 ao invés de 10. Assim todos as operações devem ser feitas em módulo 2, e os dígitos utilizados são apenas '0' e '1'.
Multiplicação de números sem sinal
Veja o exemplo da multiplicação de A x B = '1101010110' x '101101' (854 x 45).
Note que o produto é composto apenas pela seleção, deslocamento e soma do multiplicando (A). O valor do bit do multiplicador (B) indica se uma versão deslocada de A deve ser ou não selecionada para ser somada na coluna correspondente ao bit de B. Toda a multiplicação pode ser realizada utilizando somadores e uma lógica de seleção e deslocamento.
Multiplicação de números com sinal
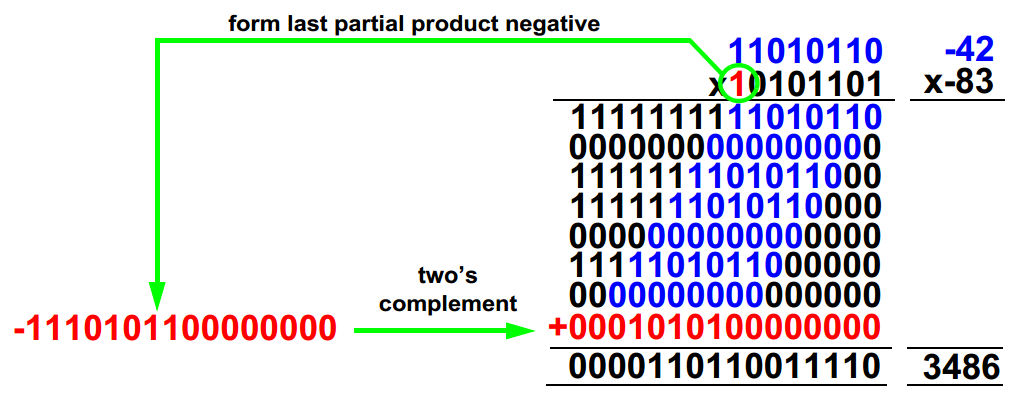
Para a multiplicação de números com sinal, estes devem ser representados em complemento de 2.
Se um dos operandos for positivo e outro negativo, utilize o operando negativo como multiplicando e o positivo como multiplicador, e faça a extensão do sinal dos resultados parciais da multiplicação.
Se ambos operandos forem negativos, faça a extensão do sinal dos resultados parciais da multiplicação, exceto no último bit (MSB), para o qual deve ser utilizado o seu valor complementado de 2.
Uma forma alternativa de fazer a multiplicação de números com sinal é realizar a operação dos valores positivos e no final fazer a correção do sinal utilizando a regra da multiplicação ('+' x '+' = '+'; '+' x '-' = '-'; '-' x '+' = '-'; '-' x '-' = '+'). Se resultado deve ser negativo, simplesmente o valor deve ser representado em complemento de 2.
Outra forma alternativa de multiplicar números binários com sinal é o Algoritmo de multiplicação de Booth.
Multiplicação de números ponto fixo
A multiplicação é semelhante as duas anteriores, apenas o número de casas fracionarias deve ser levada em conta na multiplicação.
Links externos
- Lesson 54 - Digital Multiplier - LBEbooks