PSD-CSTTel (página)
MURAL DE AVISOS E OPORTUNIDADES DA ÁREA DE TELECOMUNICAÇÕES
Link curto para esta página: http://bit.ly/PSDIFSC
Ementa e referências bibliográficas
Informações da disciplina
- PROFESSOR: Diego da Silva de Medeiros
- PLANO DE ENSINO
Diário de aula
Aulas
Apresentação da disciplina
- Nesta primeira aula, a disciplina foi apresentada. Foi falado sobre a ementa, avaliação, cronograma, etc.
Sinais em tempo discreto
Referência: Capítulo 3 do Livro do Lathi, pg. 224.
Introdução à Sinais em Tempo Discreto
- Esta aula é a introdução da disciplina.
- Um sinal discreto é uma abstração de um sinal amostrado, que por sua vez é obtido a partir da multiplicação de um sinal contínuo por um trem de impulsos. A amostragem de sinais é assunto de outra disciplina (Sinais e Sistemas e Comunicação Digital).
- Uma das medidas do tamanho de um sinal é a energia e a potência.
- Energia do sinal:
- Potência do sinal:
- Desta forma, sinais podem ser divididos em sinais de energia ou de potência
- Sinais de energia são sinais que tem energia finita, que desta forma tem potência zero.
- Sinais de potência são sinais que tem potência finita, que desta forma tem energia infinita.
- Alguns sinais não são nem de energia nem de potência
- É comum na área de processamento de sinais a realização de operações com sinais. Algumas dessas operações utilizadas em sinais discretos são:
- Deslocamento - Atraso ou avanço de um sinal no tempo.
- Reversão no tempo - Espelhamento no sinal a partir do eixo da ordenada (y)
- Alteração na taxa de amostragem
- Decimação - Redução da frequência de amostragem do sinal
- Interpolação - Aumento da frequência de amostragem do sinal
- Códigos Matlab desenvolvidos
* Simulação.m * u.m * s.m
- Exercícios (Lathi)
* Exemplo 3.1, pg. 226 * Exemplo 3.2, pg. 227 * Exercício E3.1, ppg. 226 * Exercícios E3.2, E3.3, E3.4 e E3.5, pg. 230
Funções Úteis
- Alguns sinais úteis na área de processamento de sinais digitais (Seção 3.3, pg. 230, do Lathi).
- Impulso unitário, também conhecido como Delta de Kronecker, é a versão discreta da Função Impulso, também conhecida como Delta de Dirac:
- Degrau unitário, versão discreta da Função Degrau. Muito utilizada para a limitação de sinais em um intervalo de tempo.
- Uma Função Exponencial discreta é descrita na forma , onde é o argumento da função e é inteiro. É possível escrever a função exponencial de uma outra forma, tendo em vista que a base e o argumento são constantes:
- A análise de funções exponenciais discretas é realizada baseada no valor de ou de . Iniciemos nossa análise considerando que , e por consequência , é real.
- Se , , de forma que é uma função crescente;
- Se , encontra-se entre 0 e 1, de forma que é uma função decrescente;
- Se , , de forma que é uma função constante igual a 1.
- A análise de funções exponenciais discretas é realizada baseada no valor de ou de . Iniciemos nossa análise considerando que , e por consequência , é real.
- Se é complexo, ele pode ser escrito na forma , e . Desta forma, também será complexo, ou . A análise é feita então em função de e .
- Se , a exponencial é puramente real, possuindo os três casos acima descritos;
- Se , e , sendo então uma função oscilatória complexa de módulo igual a 1 e frequência de oscilação igual a ;
- Se , e , sendo então uma função oscilatória complexa com módulo crescente e frequência de oscilação igual a
- Se , e , sendo então uma função oscilatória complexa com módulo decrescente e frequência de oscilação igual a
- Se é complexo, ele pode ser escrito na forma , e . Desta forma, também será complexo, ou . A análise é feita então em função de e .
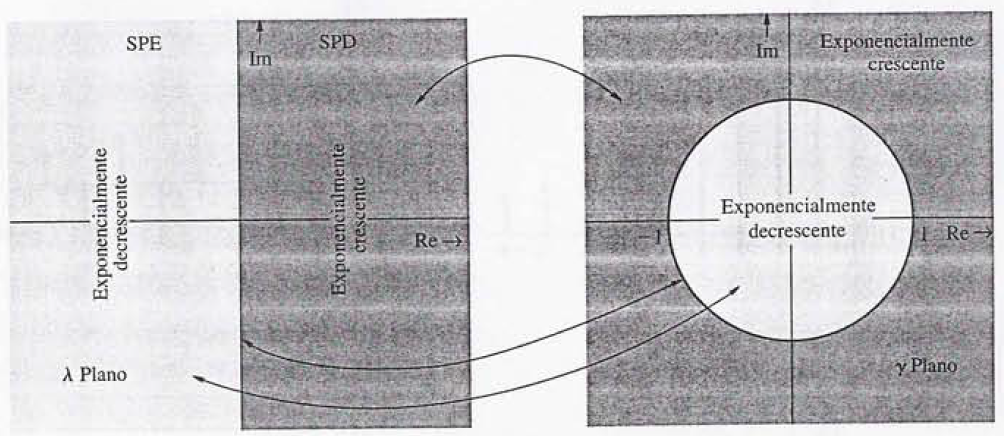
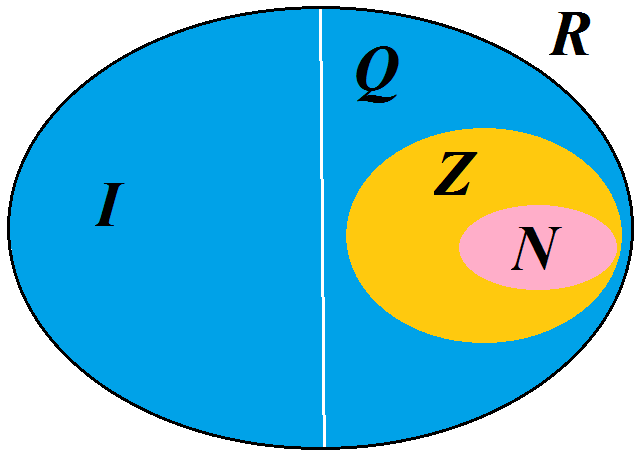
Mapeamento das funções exponenciais (retirado do livro do Lathi).
- A análise acima pode ser exportada para um gráfico, como pode ser visto na figura ao lado. Neste caso, o mapeamento de em transforma o Semi Plano Esquerdo (SPE), região onde a exponencial é decrescente, num círculo de raio unitário. O eixo das ordenadas, onde a exponencial possui módulo constante se transforma na borda do círculo. Por fim, o Semi Plano Direito (SPD), onde a exponencial é crescente, se transforma na região fora do círculo unitário.
- Códigos Matlab desenvolvidos
* Simulação.m * u.m * d.m
- Exercícios (Lathi)
* Exemplo 3.3, pg. 232 * Exercícios E3.6 e E3.7, pg. 234 * Exemplos de computador: * C3.1 para o sinal , mostrando o sinal no intervalo de 0 a 10 * C3.2 para o sinal , mostrando o sinal no intervalo de 0 a 33
Sistemas em tempo discreto
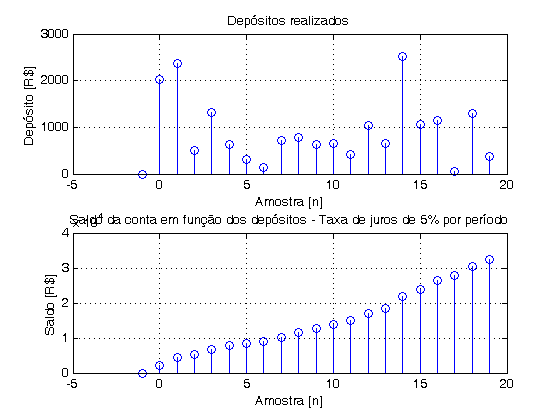
- Ao pensar em Sistemas de Tempo Discreto, normalmente vem à mente aplicações como áudio digital, imagem digital, etc. O termo discreto porém, é maior do que isso, e inclui todo sistema que é não contínuo. O exemplo abaixo, exemplo 3.4 do Lathi, aborda esta questão.
- Uma pessoa faz regularmente um depósito em um banco a um intervalo . O banco paga um certo juro na conta bancária durante o período e envia periodicamente uma correspondência com o saldo ao depositante. As variáveis envolvidas no problema são:
- = depósito feito no instante
- = saldo na conta no instante , calculado imediatamente após o recebimento do depósito
- = taxa de juros
- O saldo é a soma de:
- Saldo anterior
- Juros obtidos em durante o período
- Depósito
- A equação que relaciona a saída (saldo) com a entrada (depósito) é:
- , onde
- Ou, substituindo por
- , onde
- Uma pessoa faz regularmente um depósito em um banco a um intervalo . O banco paga um certo juro na conta bancária durante o período e envia periodicamente uma correspondência com o saldo ao depositante. As variáveis envolvidas no problema são:
- As equações anteriores, chamadas de equações diferença, relacionam a entrada e a saída de um sistema, ou de uma forma mais completa, relacionam as amostras atual e anteriores da entrada com as amostras atual e anteriores da saída. Uma versão genérica da equação diferença é:
- , com
- ou
- As equações anteriores estão na forma do operador de avanço. Substituindo por , a equação fica na forma do operador de atraso:
- , com
- Para que um sistema descrito pelas equações diferença acima descritas seja causal, é necessário que sua saída não dependa de valores futuros de sua entrada. Na forma do operador de avanço, a saída mais avançada no tempo é , e a entrada mais avançada no tempo é . Assim, para que um sistema seja causal, é necessário que
- Uma forma simples e rápida de resolver o sistema a partir da sua equação diferença é a solução recursiva (ou interativa). O método é calculado passo a passo, utilizando as condições iniciais e os valores do sinal de entrada.
Ver exemplo 3.8 do Lathi, pg. 247
- Uma forma diferente de representar o sistema é através da Notação Operacional. Nela, a equação diferença do sistema fica similar à uma equação diferencial, e um tratamento semelhante pode ser utilizado para sua resolução. Para a notação operacional, utiliza-se o operador para representar um avanço de amostras.
- Exemplo:
- Equação diferença de primeira ordem:
- Equação diferença de segunda ordem:
- Desta forma, uma equação diferença genérica em notação operacional é
- ou simplesmente
- onde
- Códigos Matlab desenvolvidos
* Simulação.m
- Exercícios (Lathi)
* Exercício 3.4-1 e 3.4-2 pg. 295 * Exemplo 3.8, pg. 247 * Exercício E3.10, pg. 249 * Exemplo de computador C3.3 para o sinal do exercício E3.10 * Descrever todas as equações diferença dos exercícios anteriores com Notação Operacional
Solução de Sistemas e Resposta de Entrada Nula
- Saída de um sistema possui componentes referentes à entrada do sistema e componentes referentes às condições iniciais
- Referentes às condições iniciais: Resposta de entrada nula
- Referentes à entrada: Resposta de estado nulo
- A resposta de entrada nula de um sistema é a solução da sua equação diferença, assumindo que não há sinais de entrada (solução homogênea).
- ou
- ou ainda
- A solução do problema é então (assumindo raízes distintas):
- onde os 's são as constantes do problema, obtidas através das condições iniciais
- Para raízes repetidas:
- e a resposta de entrada nula será:
- Para raízes complexas, expressamos as raízes na forma polar:
- e
- E a resposta de entrada nula será
- Para um sistema real
- e
- E então:
- Nomenclatura:
- = polinônio característico do sistema
- = equação característica do sistema
- = raízes características, valores característicos ou autovalores do sistema
- = modos característicos ou modos naturais do sistema
- = resposta de entrada nula do sistema, que é a combinação linear dos modos característicos
- Exercícios (Lathi)
* Exemplo 3.10, pg. 252 * Exercícios E3.11, E3.12 e E3.13, pg. 255 * Exercício de computador C3.4 para os sistemas dos outros exercícios
Resposta ao Impulso e Resposta de Estado Nulo
- Uma solução importante na análise de sistemas é a resposta do sistema à um impulso unitário. A resposta ao impulso de um sistema é a solução da sua equação diferença, considerando que há, na entrada do sistema, uma função impulso .
- Ou:
- Neste caso, considera-se todas as condições iniciais nulas:
- O método iterativo (ou recursivo) pode ser utilizado para a resolução do sistema, mas este é pouco prático para respostas longas. Por isso, há a solução fechada, dada pela equação:
- onde é a combinação linear dos modos característicos e e são obtidos da equação diferença do sistema.
Ver exemplo 3.12, pg. 258
- A resposta de estado nulo é a resposta do sistema à sua entrada, considerando suas condições iniciais zero. A solução da resposta de estado nulo é dada pelo somatório de convolução:
- onde é a entrada do sistema e é sua resposta ao impulso. Embora pareça um pouco diferente, o somatório de convolução é a mesma operação realizada em tempo contínuo, a integral de convolução.
- As propriedades do somatório de convolução são:
- Comutativa
- Distributiva
- Associativa
- Propriedade do deslocamento
- Se ,
- Convolução com um impulso
- Propriedade da largura
- Se tem elementos (amostras) e tem elementos, tem elementos.
- Causalidade
- para
- para , tal que para
- E a convolução causal é:
Ver exemplo 3.13, pg. 262
- Em geral, o cálculo da convolução propriamente dito não é muito realizado. Isso se deve à existência de tabelas com a convolução dos sinais mais comuns. Um exemplo pode ser visto na Tabela 3.1 do livro do Lathi, pg. 263.
- Mais importante que a resolução dos cálculos, seja pela equação ou pela tabela, é o entendimento do que é realizado com os sinais durante a operação. A convolução de dois sinais e inicia com a reversão no tempo de um dos sinais (por exemplo, ). Para encontrar o valor de saída para um dado instante , é deslocado de amostras, e uma multiplicação ponto a ponto é executada entre os sinais e . O processo de convolução consiste então no deslocamento de por toda a extensão de . Este fato pode ser visto em [1] e [2].
- Slides da aula
- Resolução de alguns exercícios, realizada dia 13/09
- Exercícios (Lathi)
* Exemplo 3.11, pg. 256 * Exemplo 3.12, pg. 258 * Exercício E3.14, pg. 259 * Exercício 3.7-4, pg. 298 * Exemplo 3.13, pg. 262 * Exercício E3.15, pg. 263 * Exemplo 3.14, pg. 264 * Exemplo de computador C3.6 * Criar uma função no Matlab para realizar a convolução entre dois sinais causais
Resposta Total e Estabilidade
- A Resposta total de um sistema é definida como:
- Resposta Total = Resposta de entrada nula + Resposta de estado nulo
- Resposta Total =
- A estabilidade de um sistema é dividida entre estabilidade externa (BIBO - Bounded-input/boundded-output) e interna (assintótica).
- Um sistema é BIBO estável se a sua resposta ao impulso for absolutamente somável:
- A estabilidade externa de um sistema é caracterizada da seguinte forma:
- Raízes simples ou repetidas dentro do círculo unitário: assintoticamente estável
- Raízes simples sobre o círculo unitário: marginalmente estável
- Raízes repetidas sobre o círculo unitário: assintoticamente instável
- Raízes simples ou repetidas fora do círculo unitário: assintoticamente instável
- As estabilidades interna e externa são relacionadas da seguinte forma:
- Raízes dentro do círculo são absolutamente somáveis, por isso sistemas assintoticamente estáveis são BIBO estáveis.
- Raízes sobre ou fora do círculo não são absolutamente somáveis, por isso sistemas marginalmente estáveis ou assintoticamente instáveis são BIBO instáveis.
- Exercícios (Lathi)
* Exemplo 3.22, pg. 285 * Exercício 3.10-2, pg. 303
Avaliação 1
- Os conteúdos referentes à primeira parte da disciplina (capítulo 3 do Lathi) foram avaliados através de uma prova.
Transformada Z
Referência: Capítulo 5 do Livro do Lathi, pg. 442.
Definição da Transformada Z Direta e Inversa
- A Transformada Z Direta é calculada como a seguir:
- A forma mais direta de resolução se dá considerando que os termos a serem somados são elementos de uma PG (progressão geométrica). Uma PG é definida como uma sucessão de termos:
- onde, ou , sendo denominado razão da sucessão de termos.
- A planilha a seguir foi feita para ajudar o entendimento das PGs, confirmando a equivalências das duas equações acima Link.
- Para a soma de termos de uma PG ( finito):
- Para a soma de infinitos termos de uma PG:
- Para mais informações sobre PGs, ver Link.
- A Transformada Z inversa é definida como:
- Em geral este cálculo não é realizado, dada a existência de tabelas (ver tabela 5.1 do Lathi ou esta seção da Wikipédia). O que é necessário para a resolução dos problemas é adequar o sinal no domínio Z à algum par específico da tabela.
- Exercícios (Lathi)
* Exemplo 5.1, pg. 444 * Exemplo 5.2, pg. 446 * Exercício E5.1, pg. 448 * Selecionar alguns itens do exercício 5.1-2, pg. 516 * Exercício 5.1-4, pg. 517
* Exemplo 5.3, pg. 448 * Exercício E5.2, pg. 451 * Exercício 5.1-5, pg. 517
Resolução de exercícios com a Transformada Z
- A Avaliação 1 realizada na aula passada foi discutida, bem como foram resolvidos exercícios de transformada Z direta e inversa.
- Exercícios (Lathi)
* Exemplo 5.1, pg. 444 * Exemplo 5.3.a, pg. 448
- Resoluções realizadas no semestre 2013-1
- Solução exemplo 5.3.b
- Solução exemplo 5.3.c
Propriedades da Transformada Z
- Algumas propriedades podem ser utilizadas para facilitar o cálculo da transformada Z. Exemplos de tabelas são a Tabela 5.2, pg. 459 do Lathi e esta seção da Wikipédia.
- Nesta aula, as propriedades serão derivadas.
- Exercícios (Lathi)
* Exemplo 5.4, pg. 456 * Exercício 5.2-3, 5.2-7 e 5.2-9, pg. 518
Solução de sistemas usando a Transformada Z
- A Transformada é utilizada principalmente na solução de sistemas Lineares Discretos Invariantes no Tempo (LDIT). O método é sintetizado a seguir:
- A equação diferenças é convertida para o domínio utilizando a propriedade do deslocamento à direita da Transformada Z:
- A equação algébrica no domínio é trabalhada de forma a isolar .
- Com o isolado, a equação algébrica é convertida de volta para o domínio através da Transformada Z Inversa, encontrando então a resposta total do sistema, .
- Com esta abordagem, é possível também encontrar a resposta total com as componentes de entrada nula e de estado nulo em separado. Para isso, as componentes referentes ao sinal de entrada e às condições iniciais devem ser mantidas separadas durante o trabalho algébrico.
- Uma outra utilização da Transformada Z diz respeito à Função de transferência de um sistema. A Função de Transferência é utilizada para encontrar a a resposta de estado nulo do sistema, ou mesmo a resposta total, quando o sistema não possui condições iniciais (resposta de entrada nula igual à zero):
- então:
- Dada a equação diferenças genérica:
- ou, em notação operacional:
- ou simplesmente:
- onde:
- A Função de Transferência do sistema é:
- A estabilidade do sistema pode ser obtida a partir da sua Função de Transferência. Como a Função de Transferência é uma descrição externa do sistema, pois relaciona saída e entrada, a estabilidade BIBO (externa) é encontrada. Assim, se todos os polos de estiverem dentro do círculo unitário, o sistema será BIBO estável.
- Se e não possuírem fatores comuns, o denominador de será idêntico à , e:
- sistema assintoticamente estável: Polos de , repetidos ou simples, dentro do círculo unitário
- sistema assintoticamente instável:
- (i) Ao menos um polo de fora do círculo unitário;
- (ii) Polos de repetidos sobre o círculo unitário
- sistema marginalmente estável: Nenhum polo de fora do círculo unitário e pelo menos um polo simples sobre o círculo unitário.
- Exercícios (Lathi)
* Exemplo 5.5, pg. 461 * Exercício E5.10, pg. 462 * Exercício E5.11, pg. 463 * Exercício E5.12, pg. 464 * Exercícios 5.3-2, 5.3-3, 5.3-5, 5.3-6, 5.3-7, 5.3-8, 5.3-10, pg. 519
* Exemplo 5.6, pg. 466 * Exercício 5.3-18, pg. 519 * Exercícios 5.3-19, 5.3-20, 5.3-21, 5.3-23, pg. 520
Resposta em Frequência de Sistemas em Tempo Discreto
- A Resposta em Frequência de um sistema de Tempo Discreto é encontrada a partir da sua Função de Transferência, substituindo por . Assim, a frequência é indicada por . Usando a seta direcional para representar a relação entrada saída:
- E, fazendo :
- onde é a Resposta em Frequência do sistema, que expressa na forma polar:
- Para uma entrada senoidal, considerando que é a parte real de :
- e para uma senoide defasada de :
Ver Exemplo 5.10 do Lathi, pg. 476
- Como pode ser visto no exemplo anterior, a Resposta em Frequência de Sistemas de Tempo Discreto é Periódica com período . Isto se deve à não unicidade de ondas senoidais no domínio de tempo contínuo:
- , para inteiro
- Isto pode ser confirmado pelo seguinte Código MATLAB.
- A Resposta em Frequência do sistema também pode ser determinada pela posição dos seus polos e zeros. Para uma Função de Transferência genérica:
- encontrando as raízes de ambos os polinômios, a Forma Fatorada da Função de Transferência é encontrada:
- Para encontrar a Resposta em Frequência do sistema, fazemos . Como , variar significa percorrer o círculo unitário. Desta forma, a resposta do sistema para uma determinada frequência é encontrada a partir da linha que une os polos e zeros ao ponto de ângulo sobre o círculo unitário. Ou:
- ou
- onde e são os módulos e e são os ângulos da linha que une o zero e o polo ao ponto de ângulo sobre o círculo unitário.
- Desta forma, as seguintes conclusões podem ser tomadas
- Como a magnitude de é diretamente proporcional ao produto das distâncias dos zeros à , incluir um zero próximo de um determinado ângulo do círculo unitário reduz a resposta de magnitude para esta frequência angular. Para suprimir totalmente uma determinada frequência, um zero neste ângulo do círculo unitário pode ser inserido.
- Como a magnitude de é inversamente proporcional ao produto das distâncias dos zeros à , incluir um polo próximo de um determinado ângulo do círculo unitário aumenta a resposta de magnitude para esta frequência angular. Não se deve esquecer que um polo sobre o círculo unitário resulta num sistema BIBO instável.
- Para um filtro ideal, o número de polos e zeros necessários é muito grande (infinito).
- Este comportamento pode ser visto na ferramenta do MATLAB Fdatool.
- Exercícios (Lathi)
* Exemplo 5.10, pg. 476 * Exercício E5.18, pg. 479 * Exercícios 5.5-1, 5.5-2, 5.5-4, pg. 521 * Exercícios 5.5-5, pg. 522
* Exercício 5.6-1, pg. 522
Laboratório de Transformada Z
- Este laboratório tem o objetivo de auxiliar o entendimento dos conceitos que envolvem a utilização da Transformada Z na análise e solução de sistemas LDIT. Mais precisamente, a Função de Transferência será explorada, de forma a visualizar a resposta em frequência a partir da posição dos polos e zeros do sistema.
- Pré laboratório
- Estudar o help do matlab das funções:
- polar()
- poly()
- roots()
- freqz()
- Laboratório
- Definir os seguintes sistemas com o mínimo de polos e zeros:
- Filtro passa-baixas
- Filtro passa-altas
- Filtro passa-faixa
- Filtro rejeita-faixa
- Plotar os polos (x) e os zeros (o) no círculo unitário usando a função polar()
- Calcular a resposta em frequência do filtro criado utilizando a função freqz()
- Observar a definição da frequência de amostragem nos parâmetros.
- Plotar a resposta de magnitude e de fase dos filtros
- Aumentar o número de polos e zeros dos filtros e observar o comportamento
Análise de Fourier de Sinais em Tempo Discreto
Referência: Capítulo 9 do Livro do Lathi, pg. 738.
Série de Fourier de Tempo Discreto
- Periodicidade de uma senoide discreta
- Uma senoide discreta é periódica com período inteiro se . Esta equação é verdadeira quando , com inteiro. Assim, a senoide será periódica se:
- um número racional (representado pela divisão de dois números inteiros)
- O Período Fundamental da senoide será então:
- sendo a Frequência Fundamental da senoide e o menor inteiro que faz um número inteiro.
- O Período Fundamental da senoide será então:
- Definição da Série de Fourier de Tempo Discreto
- A Série de Fourier de Tempo Discreto é constituída pela soma de exponenciais complexas e discretas, com frequências múltiplas da frequência fundamental:
- Mas como:
- A Série de Fourier de Tempo Discreto é finita, com termos.
- Mas como:
- A Série de Fourier de Tempo Discreto é definida por:
- onde é o coeficiente associado à frequência angular , definido por:
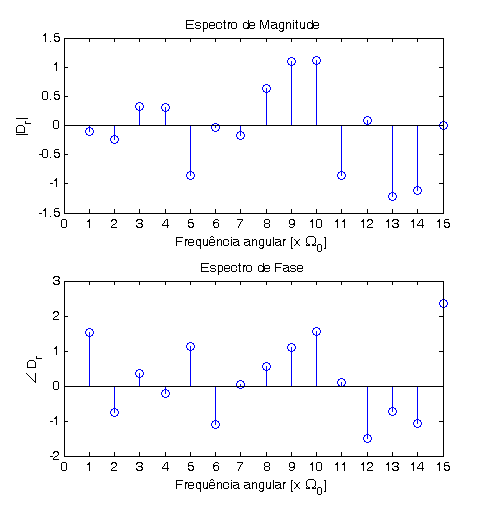
- Espectro de Fourier de um Sinal Discreto
- A Série de Fourier tem componentes:
- onde as frequências de cada componente. Considerando que é em geral complexo, na forma
- Pode-se então fazer um gráfico relacionando o módulo e a fase de com a frequência do termo. Este é o Espectro de Fourier do sinal.
- Códigos Matlab desenvolvidos
* Periodicidade_senoide.m * Espectro_Fourier.m * ExemploC9_2.m
- Exercícios (Lathi)
* Exemplo 9.2, pg. 745 * Exercício E9.2, pg. 744 * Exercício 9.1-1, 9.1-4, 9.1-5 e 9.1-6, pg. 783
Transformada de Fourier de Tempo Discreto
- As Séries de Fourier de Tempo Discreto permitem descrever sinais discretos periódicos através da soma de exponenciais complexas. Quando o sinal é aperiódico a utilização da série é inviabilizada. A extensão da análise de Fourier para sinais discretos aperiódicos é feita da mesma forma que no mundo contínuo, formando um sinal aperiódico a partir de um sinal periódico com período infinito.
- Sendo assim, o par de Transformadas de Fourier é definido como:
- Transformada Direta
- Transformada Inversa
- Informações relevantes
-
- Espectro é uma função contínua de
- Espectro é uma função periódica de :
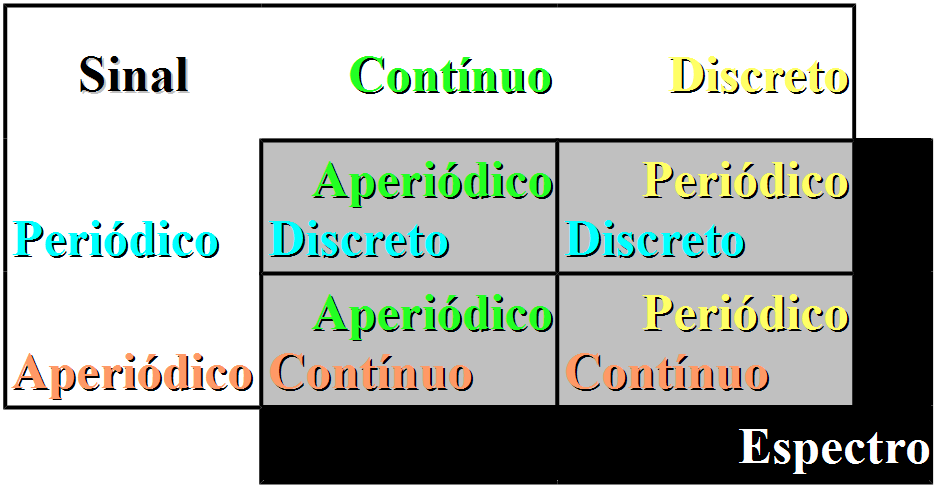
- Espectro Periódico X Amostrado
- Sinal periódico:
- Séries de Fourier
- Espectro discreto (harmônicas)
- Sinal aperiódico:
- Espectro contínuo
- Sinal discreto (amostrado)
- Espectro periódico (repetido a cada Hz ou )
- Sinal contínuo
- Espectro aperiódico
- Exercícios (Lathi)
* Exemplo 9.3, pg. 752 * Exemplo 9.4, pg. 753 * Exemplo 9.5, pg. 754 * Exemplo 9.6, pg. 756 * Exercício E9.4 e E9.5, pg. 756
Filtros Digitais
Referência: Capítulo 4, 5 e 6 do Livro do Shenoi.
Introdução aos Filtros Digitais
- Os filtros digitais processam sinais digitais.
Materiais PSD de semestres anteriores
| Clicar no "+" para expandir |
|---|
Listas de Exercício
Avaliações
Grupos de Discussão em TelecomunicaçõesAlguns assuntos correlatos
Links de auxílio
Erratas e Códigos .m
|
![{\displaystyle E_{x}=\sum _{n=-\infty }^{\infty }{\left|x[n]\right|}^{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/36d7eac8aff3508de94d746317b7b84652ddee3a)
![{\displaystyle P_{x}=\lim _{N\to \infty }{1 \over {2N+1}}\sum _{n=-N}^{N}{\left|x[n]\right|}^{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7cb94307dc2736261d2ceb0cf05fdad4b1daafb5)
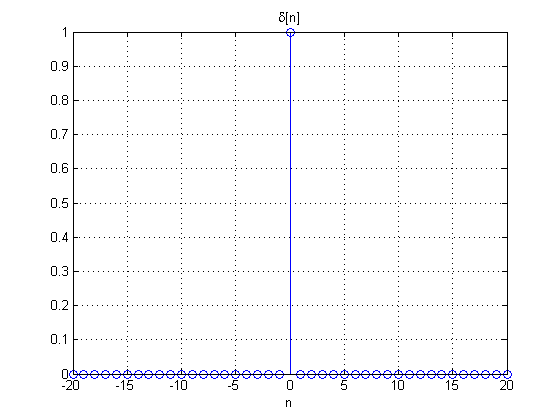
![{\displaystyle \delta [n]=\left\{{\begin{matrix}1,&{\mbox{se }}n=0\\0,&{\mbox{se }}n\neq 0\end{matrix}}\right.}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cde09c5418f2c174d7ca7a9594c512065bc649ba)
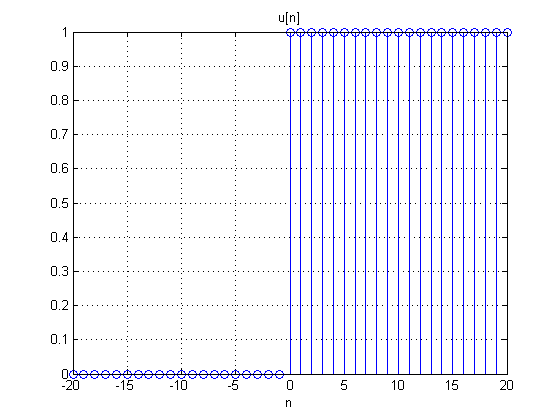
![{\displaystyle u[n]=\left\{{\begin{matrix}1,&{\mbox{se }}n\geq 0\\0,&{\mbox{se }}n<0\end{matrix}}\right.}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2b113bd05f7035be9628fa2610eb748072ab0d88)
























![{\displaystyle \gamma =e^{a}e^{jb}=e^{a}[cos(b)+jsen(b)]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8ef681ff67ae61f8424ad8ebaedd9134c74e25e3)


![{\displaystyle x_{d}[n]=(0,7)^{-n}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d59d7d4051a667e30f194dc48b838a2563e7c570)
![{\displaystyle x[n]=3cos(2\pi 0,0909n)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/757c9ea2abd2a9583db9561134496202f7c4eeab)

![{\displaystyle x[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d)
![{\displaystyle y[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/305428e6d1fb59cd0163a7a96ace52292a262afa)

![{\displaystyle y[n-1]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9862a8ad5444b16db02655c12ae0a44a1871a00e)
![{\displaystyle y[n]=y[n-1]+ry[n-1]+x[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7b1742209e98a42c01f99812b3097c579cfe98f5)
![{\displaystyle y[n]=(1+r)y[n-1]+x[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0159ed158e1201aafd3d9ea72e0c2ebcc940e394)
![{\displaystyle y[n]-ay[n-1]=x[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d48e1a93137c49ec58792802a3796a39763446d3)


![{\displaystyle y[n+1]-ay[n]=x[n+1]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/898e5732a7b8045958a8d581c7c06f2a691d8301)
![{\displaystyle \left.\sum _{k=0}^{N}a_{k}y[n+N-k]=\sum _{l=0}^{M}b_{l}x[n+M-l]\right.}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/74c65d7e6987fd877ef4ec7a4baabede7e9dc70e)

![{\displaystyle \left.y[n+N]+a_{1}y[n+N-1]+...+a_{N}y[n]=b_{0}x[n+M]+b_{1}x[n+M-1]+...+b_{M}x[n]\right.}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/087ad17f0230e81b2968664c93a39b8cac74012b)

![{\displaystyle \left.\sum _{k=0}^{N}a_{k}y[n-k]=\sum _{l=0}^{M}b_{l}x[n-l]\right.}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7e0a50ca411cc3bf279ba9442e1885fd89753b89)
![{\displaystyle y[n+N]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/63a2c1d2c066692c3821eab1a747e38427759ef9)
![{\displaystyle x[n+M]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/270cd415d1ad185490917ea24e00969bcfc74184)


![{\displaystyle {\begin{matrix}Ex[n]&{}:={}&x[n+1]\\E^{2}x[n]&{}:={}&x[n+2]\\{}&\vdots &{}\\E^{N}x[n]&{}:={}&x[n+N]\end{matrix}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2ff62ebe23b4dea33b5d635425074d80e3c0f801)
![{\displaystyle {\begin{matrix}y[n+1]-ay[n]&{}={}&x[n+1]\\Ey[n]-ay[n]&{}={}&Ex[n]\\(E-a)y[n]&{}={}&Ex[n]\end{matrix}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/daf078b71b20b341b17ce7a9c5f33245646ee5cb)
![{\displaystyle {\begin{matrix}y[n+2]+{\frac {1}{4}}y[n+1]+{\frac {1}{16}}y[n]&{}={}&x[n+2]\\(E^{2}+{\frac {1}{4}}+{\frac {1}{16}})y[n]&{}={}&E^{2}x[n]\end{matrix}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/83372ed4b9e3f717c6e41ba8ea47d58d65636c23)
![{\displaystyle \left(E^{N}+a_{1}E^{N-1}+...+a_{N-1}E+a_{N}\right)y[n]=\left(b_{0}E^{N}+b_{1}E^{N-1}+...+b_{N-1}E+b_{N}\right)x[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3d5c2a6ca591349928c765d04dfe1943cd64f881)
![{\displaystyle Q\left[E\right]y[n]=P\left[E\right]x[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/510732922035500fd4e01bd8619eb241868d1300)
![{\displaystyle Q\left[E\right]=E^{N}+a_{1}E^{N-1}+...+a_{N-1}E+a_{N}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/65e72d8d0c7c25ccd06f71a789715fa0ce292f24)
![{\displaystyle P\left[E\right]=b_{0}E^{N}+b_{1}E^{N-1}+...+b_{N-1}E+b_{N}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e848c908d06d7398df2ca479e6169208a23edd75)
![{\displaystyle \left.Q[E]y_{0}[n]=0\right.}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f1bf422af648d3e9d5a05c72d54873ed425c3b96)
![{\displaystyle \left(E^{N}+a_{1}E^{N-1}+...+a_{N-1}E+a_{N}\right)y_{0}[n]=0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/aaf79b88547450699772fc77ccbbdc8a72ba6303)
![{\displaystyle \left.y_{0}[n+N]+a_{1}y_{0}[n+N-1]+...+a_{N}y_{0}[n]=0\right.}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1f47806f0d4766ce1619bf8848caf505cb73291e)
![{\displaystyle y_{0}\left[n\right]=c_{1}\gamma _{1}^{n}+c_{2}\gamma _{2}^{n}+...+c_{N}\gamma _{N}^{n}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e5bdb5520d800bc410726f194382d9c6429beae0)

![{\displaystyle \left.Q[\gamma ]=(\gamma -\gamma _{1})^{r}\right.}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/879292fd3efebd76fe3c7871843b05b7e6c6a5d4)
![{\displaystyle y_{0}\left[n\right]=(c_{0}+c_{1}n+c_{2}n^{2}...+c_{r-1}n^{r-1})\gamma _{1}^{n}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/46d6aa801c8bb09cc71c1ae146f1f684b270f1ed)


![{\displaystyle y_{0}^{}[n]=c_{1}\gamma ^{n}+c_{2}(\gamma ^{*})^{n}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/bf6530515453e6d5d8b2970bc32242862920643e)


![{\displaystyle y_{0}[n]={\frac {c}{2}}\alpha ^{n}cos(\beta n+\theta )}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ec4819fe9451c8938ca5714136f2be518b65be55)
![{\displaystyle Q[\gamma ]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/510f6a1ff42bc8244d9b89a0edc2eda2011cfd5b)
![{\displaystyle Q[\gamma ]=0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a3b9be28ac2da48c896ac443a85a9e591a9f3353)


![{\displaystyle y_{0}[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/34444a7f1aec23f75ba11a12b8621e18761ee1ee)
![{\displaystyle h[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/89981bbbb05ffd469eeadb828c18359965985e46)
![{\displaystyle \delta [n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f2a6caf535cb44fa3526b2f320330a805edfdfaa)
![{\displaystyle Q\left[E\right]h[n]=P\left[E\right]\delta [n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/327be95aa42b8e6df877e9fe659b974c03d0465d)
![{\displaystyle h[-1]=h[-2]=...=h[-N]=0_{}^{}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b2922e98f1b5e667bf56f93e8469a7012fb2afc3)
![{\displaystyle h[n]={\frac {b_{N}}{a_{N}}}\delta [n]+y_{c}[n]u[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/863dda49371d92be76f98046d396ae3a12b1bf7f)
![{\displaystyle y_{c}[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d23bad3deb7ed7ea5484da8c4acdfc02fb2fbe24)


![{\displaystyle y[n]=x[n]*h[n]=\sum _{m=-\infty }^{\infty }x[m]h[n-m]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/73f4f905e9395ee717396a3846fa285b56efee5f)
![{\displaystyle x_{1}[n]*x_{2}[n]=x_{2}[n]*x_{1}[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/29184a31bbaf093b9a55e3fa51b5a0d237102c9f)
![{\displaystyle x_{1}[n]*(x_{2}[n]+x_{3}[n])=x_{1}[n]*x_{2}[n]+x_{1}[n]*x_{3}[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/359368cab158126a20a01174fa6c7c4d6ff35df9)
![{\displaystyle x_{1}[n]*(x_{2}[n]*x_{3}[n])=(x_{1}[n]*x_{2}[n])*x_{3}[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/056e048a64c0ad3aa2e82632ad610569f2185b8a)
![{\displaystyle x_{1}[n]*x_{2}[n]=c[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f5303a017cf1d581da4a21c0b7171b3895816061)
![{\displaystyle x_{1}[n-m]*x_{2}[n-p]=c[n-m-p]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a771f99e20e9302103263f4cdc29e092d51ff94d)
![{\displaystyle x[n]*\delta [n]=x[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/723678a4dbf0cbd22ad3a2bd503dd40e788cc8ad)
![{\displaystyle d[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e610d48c9dc39a27fcc5075b2ccd1328664fd219)

![{\displaystyle e[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9333d516ef86093cecb2ccbbc8097e5136758c0d)

![{\displaystyle f[n]=d[n]*e[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/778c97008b916df773e956ae339a8fc6335844c3)

![{\displaystyle x[m]=0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3eb6a9a31e0d94ce486123c7ce168c87e8e5bdfe)

![{\displaystyle h[m]=0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/123ba7ba69f626efb2363e042e145a09f6a4a7ec)
![{\displaystyle h[n-m]=0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/50c251ee48adeaa7655ea2947dc90b4925d13fd7)

![{\displaystyle y[n]=x[n]*h[n]=\sum _{m=0}^{n}x[m]h[n-m]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b11914bd7ff7144073dcd5b1a61f4f446ed94fad)
![{\displaystyle x[m]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2571c77d494efae134b6a5904b70d02c27b5e961)
![{\displaystyle h[m]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4bf03cff26a0e13bbd17cf88ee7b46b05c3df090)
![{\displaystyle x[-m]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4eeb700a3317c1a38087307b4d68efd39d8f2aa0)
![{\displaystyle x[-m+n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d89b1ca686e50612ca4ba28774d22ff369fb1185)
![{\displaystyle \sum _{j=1}^{N}c_{j}\gamma _{j}^{n}+x[n]*h[n]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e3947878e1d1dd0663e16741c250233556f5a40f)
![{\displaystyle \sum _{n=-\infty }^{\infty }|h[n]|<K<\infty }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5e847f0cd6c1f4ad09d55a0cf1af95848c3b2f62)
![{\displaystyle X[z]=\sum _{n=-\infty }^{\infty }x[n]z^{-n}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/568fafa157ba8d6cb45167766d604e81c0eb7887)






![{\displaystyle x[n]={\frac {1}{2\pi j}}\oint X[z]z^{n-1}dz}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6dd369e22aa04bd5bb23073c030bec09e5e01d12)

![{\displaystyle x[n-m]u[n]\Leftrightarrow {\frac {1}{z^{m}}}X[z]+{\frac {1}{z^{m}}}\sum _{k=1}^{m}x[-k]z^{k}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b194a475e6e161141fe1fb3e8d753e939c363f83)
![{\displaystyle Y[z]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f8c308bd420dcb4d029c2b4769a2d5a8d6acf8b0)
![{\displaystyle Y[z]=X[z]H[z]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5002486e506d5e6123a770d3cc0eb7714422746a)
![{\displaystyle H[z]={\frac {Y[z]}{X[z]}}={\frac {\mbox{Resposta total}}{\mbox{Entrada}}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f76926fc25ecae04cd823b1490abc740f589f552)
![{\displaystyle H[z]={\frac {P[z]}{Q[z]}}={\frac {b_{0}z^{N}+b_{1}z^{N-1}+...+b_{N-1}z+b_{N}}{z^{N}+a_{1}z^{N-1}+...+a_{N-1}z+a_{N}}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4f31f9f2cefec83ec89a39b2847e51fcba3c1dbb)
![{\displaystyle H[z]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e7a77a7ca1ca5b22e6333ca54be0630944c2bee4)
![{\displaystyle P[z]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/976d993df84b4c88421fbe7c584500777b9ae6f4)
![{\displaystyle Q[z]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/be9ba1ec47a6af086d320184ccede2df2c7ea957)




![{\displaystyle z^{n}\Rightarrow H[z]z^{n}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7f189d769958ca6ff1c326825c6499811bf5eb36)

![{\displaystyle e^{j\Omega n}\Rightarrow H[e^{j\Omega }]e^{j\Omega n}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f2320a3ae4e22dfd313b4b5a79b55198ebac98c8)
![{\displaystyle H[e^{j\Omega }]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d7766bf937e5afc3c4c43224b67a7b23f0f953f2)
![{\displaystyle H[e^{j\Omega }]=|H[e^{j\Omega }]|e^{j\angle {H[e^{j\Omega }]}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d541fc734de394fdd9e18627bbe52c2e0db92716)


![{\displaystyle \cos(\Omega n)\Rightarrow \Re (H[e^{j\Omega }]e^{j\Omega n})}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/497a33c6844b27a89347a5954412329fcaec7b0a)
![{\displaystyle \cos(\Omega n)\Rightarrow |H[e^{j\Omega }]|\cos(\Omega n+\angle {H[e^{j\Omega }]})}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ca436bc71c885e27197dbf3281844f72306e4d74)

![{\displaystyle \cos(\Omega n+\theta )\Rightarrow |H[e^{j\Omega }]|\cos(\Omega n+\theta +\angle {H[e^{j\Omega }]})}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/76ad826c9d3dae41659ac7a73c381a5e32a0cfa7)

![{\displaystyle \cos[(\Omega +-2\pi m)n]=\cos(\Omega n)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5fbbb6ab92b233546c842428eac590017658d733)

![{\displaystyle H[z]={\frac {b_{0}z^{N}+b_{1}z^{N-1}+...+b_{N-1}z+b_{N}}{z^{N}+a_{1}z^{N-1}+...+a_{N-1}z+a_{N}}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/083766f8b1f515779e4c38268105dd593e8bc8d7)

![{\displaystyle H[z]=b_{0}{\frac {(z-z_{1})(z-z_{2})...(z-z_{N})}{(z-\gamma _{1})(z-\gamma _{2})...(z-\gamma _{N})}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/475523e536aa45a5dd3c323bf908dd02eacdab8e)

![{\displaystyle H[e^{j\Omega }]=b_{0}{\frac {(r_{1}e^{j\phi _{1}})(r_{2}e^{j\phi _{2}})...(r_{N}e^{j\phi _{N}})}{(d_{1}e^{j\theta _{1}})(d_{2}e^{j\theta _{2}})...(d_{N}e^{j\theta _{N}})}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/81a7a2b189291544eecc60a47dc708c38c587d3b)
![{\displaystyle H[e^{j\Omega }]=b_{0}{\frac {r_{1}r_{2}...r_{N}}{d_{1}d_{2}...d_{N}}}e^{j[(\phi _{1}+\phi _{2}+...+\phi _{N})-(\theta _{1}+\theta _{2}+...+\theta _{N})]}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/740dadffaa75359849050fa3256a2505193ea6d8)








![{\displaystyle \cos[\Omega _{0}(n+N_{0})]=\cos(\Omega _{0}n)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5815c97820650a1e167a89b8c4ce0a931cafa23d)






![{\displaystyle x[n]=\sum _{r=0}^{N_{0}-1}D_{r}e^{jr\Omega _{0}n}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/dd500fbdb63f5d14ef47b595cc7cc8f8d029c47b)


![{\displaystyle D_{r}={\frac {1}{N_{0}}}\sum _{k=0}^{N_{0}-1}x[k]e^{-jr\Omega _{0}k}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/34b67f6612f88a6e5cc0b04bda58058e0fd5f14f)



![{\displaystyle x(\Omega )=\sum _{n=-\infty }^{\infty }x[n]e^{-j\Omega n}\Rightarrow {}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/180e32406efc3ee7bdb82c79175a3d87ec108316)
![{\displaystyle x[n]={\frac {1}{2\pi }}\int _{2\pi }X(\Omega )e^{j\Omega n}d\Omega \Rightarrow {}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/68885eacb09c6b8724e020f1edb59d535d3820b7)
![{\displaystyle X(\Omega +2\pi )=\sum _{n=-\infty }^{\infty }x[n]e^{-j(\Omega +2\pi )n}=\sum _{n=-\infty }^{\infty }x[n]e^{-j\Omega n}e^{-j2\pi n}=X(\Omega )}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4e016a5ef52cad912a44ee42f4755b5a614eb26d)