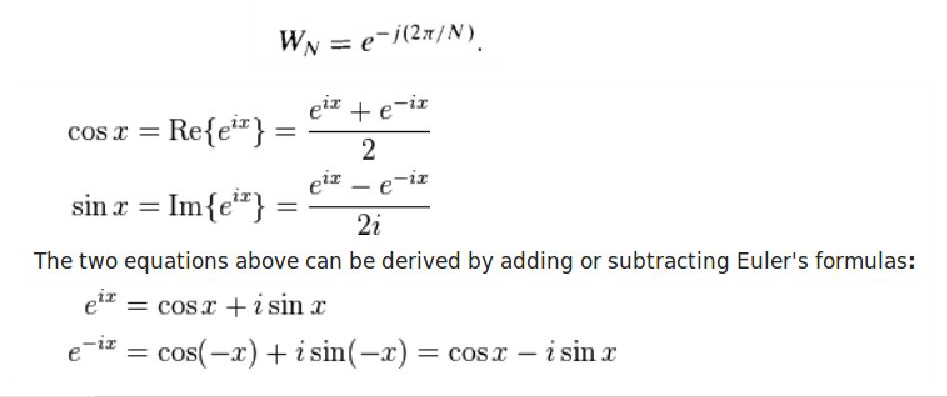Resumo do projeto
Este projeto pretende-se realizar um trabalho de pesquisa que visa estudar a utilização do ambiente Simulink® associado ao HDL (Hardware Description Language) Coder, para a realização em hardware programável, especificamente FPGA (Field Programmable Gate Array), de blocos comumente utilizados em sistemas de telecomunicações. São objetivos do projeto o estudo do Simulink®, HDL Coder e HDL Verifier da Matworks. O desenvolvimento de blocos comumente utilizados em sistemas de telecomunicações tais como moduladores, filtros digitais, misturadores e geradores de sinal, utilizando para tal o Simulink, que é um ambiente de diagramas de blocos para a simulação de projetos baseados em modelos. A realização e teste destes blocos em hardware será feita através da conversão de código para VHDL utilizando os toolboxes HDL Coder e HDL Verifier e Modelsim da ALTERA. A síntese e programação dos blocos desenvolvidos em FPGA será realizada utilizando o software Quartus II da ALTERA.
Introdução e Justificativa da Proposição
A maioria dos setores que de produção de equipamentos eletrônicos, especialmente na área de telecomunicações utilizam nos circuitos eletrônicos digitais. Entre estes circuitos a maioria deles atualmente é implementada em hardware utilizandose ASICs (Application Specific Integrated Circuits), DSPs (Digital Signal Processor) ou FPGAs (Field Programmable Gate Array). O projeto, simulação e síntese dos últimos dois tipos é realizada utilizandose ambientes de projeto assistido por computador (por exemplo Quartus II e Modelsim) e alguma linguagem de descrição de hardware (por exemplo Verilog ou VHDL) a qual permite descrever o circuito em um baixo nível, de modo a descrever até a ligação entre os componentes configuráveis nos FPGAs ou ASICs. Como a disponibilização de circuitos lógicos programáveis tais como os FPGAs a um custo cada vez mais baixo (menor que U$50,00), e velocidades crescentes de operação, está ocorrendo um grande aumento no interesse e aplicação dessa tecnologia de hardware em diversos aplicações anteriormente realizadas através de software ou eletrônica discreta. Empresas do setor de equipamentos de telecomunicações passaram a considerar essa tecnologia como uma possibilidade de implementação de grandes partes dos sistemas.
Objetivos do projeto:
- Primeira etapa - Utilizar o ambiente Simulink® para a modelagem e simulação de blocos comumente utilizados em sistemas de telecomunicações.
- Segunda etapa - Utilizar o HDL Coder e Verifier para a transformação dos blocos da primeira etapa em linguagem VHDL.
- Os circuitos da obtidos serão simulados utilizando ModelSim
- Terceira etapa - Os circuitos da segunda etapa serão sintetizados e programados no hardware programável do tipo FPGA.
- Aqui também serão feitos os testes finais.
Metodologia do projeto
- Estudo do Simulink®
- Estudo da sua configuração, interfaces, sinais, blocos, modelagem e simulação de sistemas, geração de código de software e hardware.
- Esta etapa será baseada na leitura de manuais e também sites de ajuda do próprio fabricante (MATHWORKS, 2015a, 2015c, 2015b).
- Estudo das bases da linguagem VHDL
- Esta etapa será baseada na leitura dos capítulos 18 e 19 de (PEDRONI, 2010).
- Estudo do HDL Coder e Verifier®
- Esta etapa será baseada na leitura de manuais e também sites de ajuda do próprio fabricante (MATHWORKS, 2015a, 2015c, 2015b).
- Análise de blocos disponibilizadas
- Analisar blocos disponibilizados por outras universidades e institutos de pesquisa (NAVAS, 2014; TYAGI, 2012; GIORDANO; LEVESQUE, 2015; KRUKOWSKI; KALE, 2011) na área de telecomunicações.
- Desenvolvimento de blocos para sistemas de telecomunicações
- Desenvolvimento de blocos tais como moduladores, filtros digitais, misturadores e geradores de sinal.
- Realização e teste em hardware FPGA
- Utilizando o HDL Coder para a conversão dos blocos para VHDL.
- A implementação será realizada utilizando um kit de desenvolvimento de FPGA.
- Para os testes finais tanto o SignalTap® da ALTERA como um equipamento analisador lógico externo serão necessários.
- Documentação do projeto
- Escrita de relatórios parciais e do relatório final do projeto.
- Preparação de pôster para apresentação em eventos do IFSC, e de artigo para submissão em revista.
- Gerenciamento do projeto
Implementação - FFT utilizando simulink
Arquivos das versões da FFT: Versões FFT
Documentação das modificações da FFT: Versões
- Versão 3_0 - ultima versão
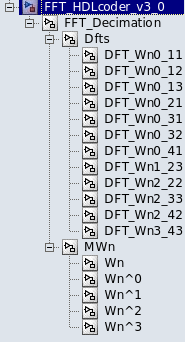
Uma visão geral dos blocos:
Figura 1 - Visão macroscópica da FFT
Blocos da FFT
Bloco - "FFT Decimation"
O bloco FFT Decimation é um subsistema que agrupa os subsistemas Dfts e Mwn. Na versão atual (3.0) as entradas são {x0_ENTRY .. x7_ENTRY} para 8 amostras temporais do sinal. As saídas no domínio transformado são {X0 .. X7}. Para a utilização do subsistema é necessário dividir o sinal de entrada em quadros de 8 amostras paralelas e processá-las. Para possibilitar uma melhor resolução de frequência da FFT é necessário aumentar o número de amostras do sinal no tempo, e para tal será desenvolvido um desserializador e um serializador para permitir o uso de entradas e saídas seriais, nas quais as amostras entram sequencialmente formando um quadro de N amostras.
Figura 1 - Composição do Bloco - "FFT Decimation
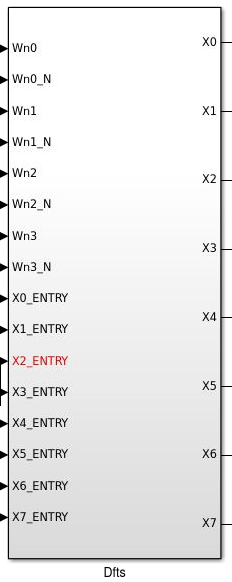
Bloco - "Dfts"
O bloco Dfts realiza os cálculos das butterflies através de pequenas células (ver figura). O subsistema Dfts possui 16 entradas, sendo 8 correspondentes as amostras temporais do sinal de entrada do bloco FFT Decimation, e 8 correspondentes ao valores calculados de Wn (mostrado abaixo). Esse bloco é implementado através de 12 blocos idênticos (células {DFT_Wn0_11 .. DFT_Wn043}) que realizam o cálculo da butterfly. As saídas do ....
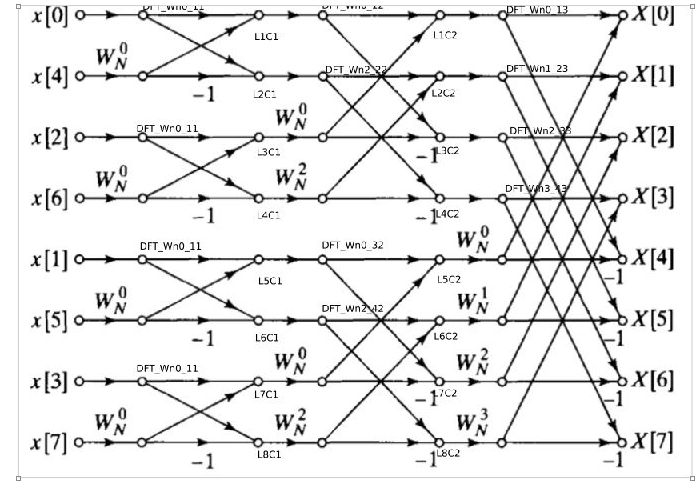
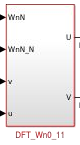
Em conjunto, os blocos do dft calculam as butterflies de acordo com a figura 5. A célula recebe quatro entradas: ({u, v}) e ({WnN, WnN_N}). As entradas ({u, v}) vem ou da entrada inicial do FFT Decimation ou da saída de uma outra butterfly. Os valores de {WnN, WnN_N} são oriundos do bloco Mwn, que será explicado mais adiante.
Figura 4 - Bloco-célula de uma butterfly
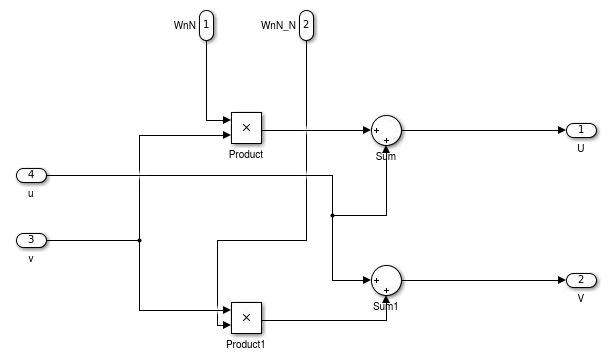
As quatro entradas se relacionam de acordo com a figura 5. A entrada v é multiplicada por WnN e por WnN_N. Os dois resultados gerados são somados com a entrada u. A butterfly gera, no fim, uma saída U e uma saída V, que poderá ser a saída final da FFT ou pode ser cascateada para outra butterfly.
Figura 5 - Esquema interno butterfly
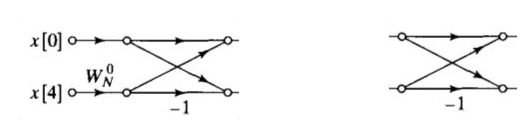
O procedimento que ocorre dentro da butterfly pode ser descrito, didaticamente, de acordo com a figura 6.
Figura 6 - Funcionamento didático butterfly
Bloco - "Mwn"
O segundo grande bloco do subsystem FFT Decimation é o Mwn. Esse bloco é o responsável pelo cálculo dos Wn do sistema.
|
|
Figura 7 - Mwn e sua estrutura interna
|
O subsistema Mwn possui apenas saídas. São 8 saídas que correspondem aos Wn calculados. Na versão 3_0 possui uma constante chamada constant8 que vale (1/8), mas na verdade ela representa 1/N, porém, essa versão comporta apenas 8 entradas, por isso optou-se por uma constante de valor 1/8. Em futuras versões esse bloco irá ter 1 entrada que irá corresponder ao N (número de entradas). A figura 7 representa uma visão geral do bloco Mwn.
Bloco - "Wn"
O bloco Wn possui 1 entrada (1:N) e uma saída (Wn). A Figura 8 demonstra sua visão macroscópica e a figura 9 representa seu esquema interno.
Figura 8 - Visão Macroscópica de Wn
- Esqueleto interno do bloco Wn:
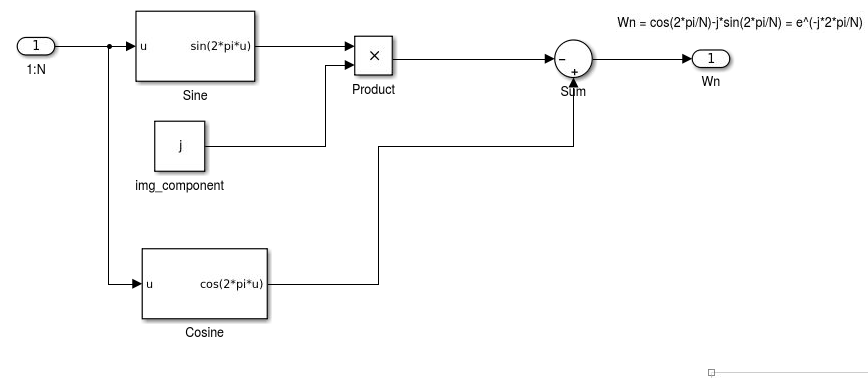
Figura 9 - Esquema interno Wn
- Para se adequar ao HDL Coder, foi necessário utilizar a estratégia apresentada na figura 10:
Figura 10 - Desmembramento de Wn
O formato padrão de cálculo do Wn se dá por um e elevado a uma função de N, porém, os blocos disponíveis no HDL coder não suportam o uso de potências de funções. A solução para esse problema foi desmembrar a função Wn em cosseno e seno, além de utilizar equivalências da fórmula de euler, como descrito na figura 10.
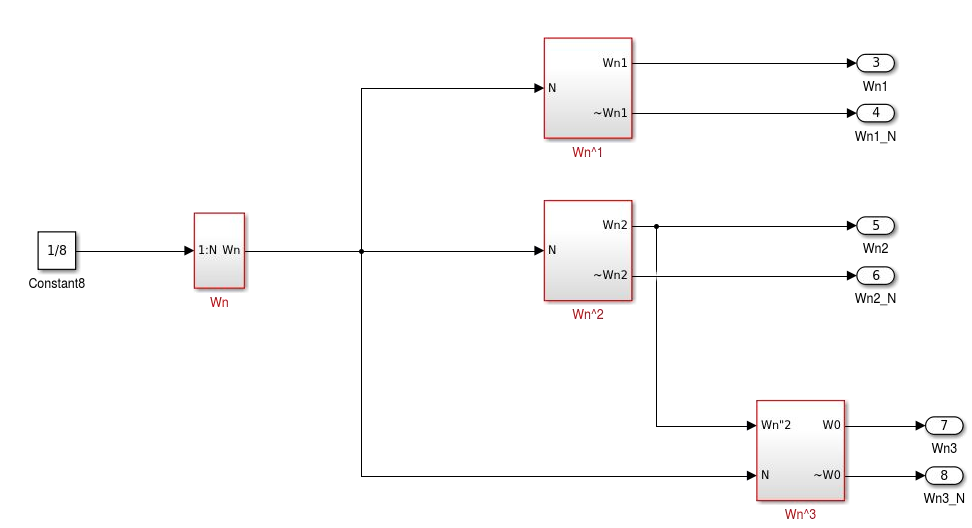
Blocos - "{Wn^0 .. Wn^3}"
Dentro do Mwn existem 4 blocos responsáveis pelas potências de Wn (Wn^0, Wn^1, Wn^2, Wn^3).
Bloco Wn^0:
Figura 11 - Visão macroscópica Wn^0
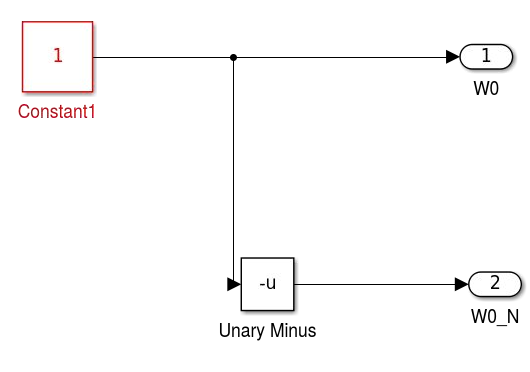
A estratégia menos custosa encontrada para resolver o cálculo de Wn^0 foi levar em consideração que qualquer número elevado a zero é igual a 1. Como descrito na imagem 12, percebe-se que o bloco em questão não possui entradas. Isso ocorre pelo mesmo motivo descrito anteriormente. Não importa qual o valor de Wn, já que o único valor possível será 1. O bloco possui 2 saídas: W0 e W0_N. O W0 corresponde ao Wn^0 original e o W0_N corresponde ao Wn^0 negado. Para calcular a parte negada, foi usado o bloco unary minus, que nada mais é do que um inversor.
Esquema interno Wn^0:
Figura 12 - Esquema interno Wn^0
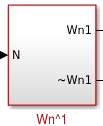
Bloco Wn^1:
Figura 13 - Visão macroscópica Wn^1
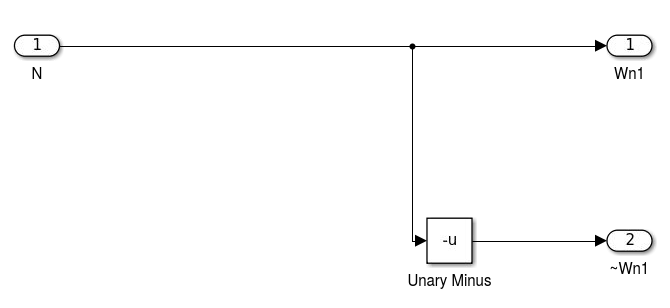
O bloco Wn^1 segue quase o mesmo esquema do Wn^0. O bloco possui 1 entrada que corresponde ao valor de Wn calculado no bloco Wn. Como esse bloco é Wn^1, sabemos que todo número elevado a 1 é igual a ele mesmo, portanto, o valor de Wn^1 será sempre ele mesmo. Assim como no bloco Wn^0, esse bloco possui 2 saídas: Wn1 e ~Wn1. Wn1 corresponde ao valor original de Wn^1 e ~Wn1 é o seu valor negado. Foi utilizado a mesma estratégia do unary minus. Se esquema é representado na figura 14.
Esquema interno Wn^1:
Figura 14 - Esquema interno Wn^1
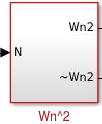
Bloco Wn^2:
Figura 15 - Visão macroscópica Wn^2
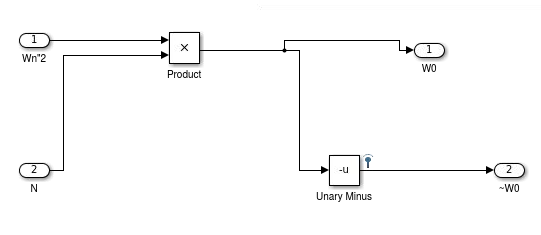
No bloco Wn^2 foi utilizada uma estratégia um pouco diferente dos blocos anteriores. Como já explanado anteriormente, o HDL coder não possui suporte para potências, portanto, o cálculo de Wn^2 necessita de algum estratégia para fazer essa potência. Sabemos que Wn^2 = Wn*Wn, logo, podemos utilizar a única entrada do bloco e conjunto com um bloco product para multiplicar a entrada N (que corresponde ao Wn calculado no bloco Wn) e obter o mesmo resultado de Wn^2. O bloco Wn^2 também possui 2 saídas: Wn2 e ~Wn2. Wn2 corresponde ao valor original de Wn^2 e ~Wn2 é o seu valor negado. Foi utilizado a mesma estratégia do unary minus. Seu esquema é representado na figura 16.
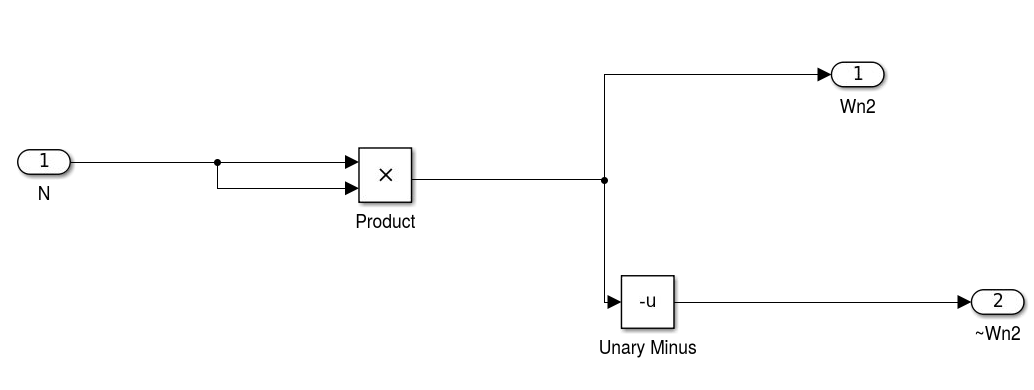
Esquema interno Wn^2:
Figura 16 - Esquema interno Wn^2
Bloco Wn^3:
Figura 17 - Visão macroscópica Wn^3
O bloco Wn^3 possui uma estratégia para que seja poupado hardware. Sabemos que Wn^3 = Wn*Wn*Wn. Seria natural utilizar 2 blocos products para realizar essa operação, porém, podemos pegar a saída Wn2 e cascatear para esse bloco. Como Wn2 foi calculado como Wn*Wn, precisamos apenas fazer Wn2*Wn e iremos obter Wn3. Essa estratégia é descrita na figura 18. O bloco Wn^3 também possui 2 saídas: Wn3 e Wn3_N. Wn3 corresponde ao valor original de Wn^2 e Wn3_N é o seu valor negado. Foi utilizado a mesma estratégia do unary minus. Seu esquema é representado na figura 18.
Esquema interno Wn^3:
Figura 18 - Esquema interno Wn^3
| Modulações Analógicas (AM,FM,PM)
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Sine Wave
|
Sim
|
Sim
|
| Scope
|
Sim
|
Sim
|
| Goto
|
Sim
|
Sim
|
| From
|
Sim
|
Sim
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Analog Passband Modulation
|
Não
|
Não
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Spectrum Analyser
|
Sim
|
Sim
|
|
| Amostragem de sinais
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Sine Wave
|
Sim
|
Sim
|
| Product
|
Sim
|
Sim
|
| Pulse Generator
|
Não
|
Não
|
| Scope
|
Sim
|
Sim
|
| Mux
|
Sim
|
Sim
|
| Gain
|
Sim
|
Sim
|
| Goto
|
Sim
|
Sim
|
| From
|
Sim
|
Sim
|
| Matrix Concatenate
|
Sim
|
Sim
|
| Manual Switch
|
Não
|
Não
|
| Zero-Order Hold
|
Sim
|
Sim
|
| DSP System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Spectrum Analyser
|
Sim
|
Sim
|
| Analog Filter Design
|
Não
|
Não
|
| From Multimedia File
|
Não
|
Não
|
| To Multimedia File
|
Não
|
Não
|
|
| Quantização
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Sine Wave
|
Sim
|
Sim
|
| Pulse Generator
|
Não
|
Não
|
| Scope
|
Sim
|
Sim
|
| Mux
|
Sim
|
Sim
|
| Goto
|
Sim
|
Sim
|
| From
|
Sim
|
Sim
|
| Zero-Order Hold
|
Sim
|
Sim
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| A-Law Expander
|
Não
|
Não
|
| A-Law Compressor
|
Não
|
Não
|
| Mu-Law Expander
|
Não
|
Não
|
| Mu-Law Compressor
|
Não
|
Não
|
| DSP System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Analog Filter Design
|
Sim
|
Sim
|
| Scalar Quantizer Encoder
|
Sim
|
Sim
|
| Sample and Hold
|
Não
|
Não
|
|
| Modulação por Codificação de Pulso (PCM)
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Sine Wave
|
Sim
|
Sim
|
| Pulse Generator
|
Não
|
Não
|
| Scope
|
Sim
|
Sim
|
| Goto
|
Sim
|
Sim
|
| From
|
Sim
|
Sim
|
| Zero-Order Hold
|
Sim
|
Sim
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Integer to Bit Converter
|
Não
|
Não
|
| DSP System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| From Multimedia File
|
Não
|
Não
|
| To Multimedia File
|
Não
|
Não
|
| Sample and Hold
|
Não
|
Não
|
| Analog Filter Design
|
Não
|
Não
|
| Scalar Quantizer Encoder
|
Não
|
Não
|
| Scalar Quantizer Decoder
|
Não
|
Não
|
{{Collapse bottom}
| Modulação Delta (DM)
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Sine Wave
|
Sim
|
Sim
|
| Pulse Generator
|
Não
|
Não
|
| Scope
|
Sim
|
Sim
|
| Goto
|
Sim
|
Sim
|
| From
|
Sim
|
Sim
|
| Sum, Add Subtract
|
Sim
|
Sim
|
| Zero-Order Hold
|
Sim
|
Sim
|
| Quantizer
|
Não
|
Não
|
| Gain
|
Sim
|
Sim
|
| Unit Delay
|
Sim
|
Sim
|
| DSP System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Analog Filter Design
|
Não
|
Não
|
| Sample and Hold
|
Não
|
Não
|
| From Multimedia File
|
Não
|
Não
|
| To Multimedia File
|
Não
|
Não
|
|
| Modulação Delta-Sigma
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Sine Wave
|
Sim
|
Sim
|
| Pulse Generator
|
Não
|
Não
|
| Scope
|
Sim
|
Sim
|
| Goto
|
Sim
|
Sim
|
| From
|
Sim
|
Sim
|
| Discrete-Time Integrator
|
Sim
|
Sim
|
| Zero-Order Hold
|
Sim
|
Sim
|
| Quantizer
|
Não
|
Não
|
| Gain
|
Sim
|
Sim
|
| Unit Delay
|
Sim
|
Sim
|
| DSP System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Analog Filter Design
|
Não
|
Não
|
| From Multimedia File
|
Não
|
Não
|
| To Multimedia File
|
Não
|
Não
|
|
| Modulação por Codificação Diferencial de Pulso(DPCM)
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Sine Wave
|
Sim
|
Sim
|
| Pulse Generator
|
Não
|
Não
|
| Scope
|
Sim
|
Sim
|
| Goto
|
Sim
|
Sim
|
| From
|
Sim
|
Sim
|
| Sum
|
Sim
|
Sim
|
| Product
|
Sim
|
Sim
|
| Zero-Order Hold
|
Sim
|
Sim
|
| Quantizer
|
Não
|
Não
|
| Gain
|
Sim
|
Sim
|
| Unit Delay
|
Sim
|
Sim
|
| DSP System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Analog Filter Design
|
Não
|
Não
|
| From Multimedia File
|
Não
|
Não
|
| To Multimedia File
|
Não
|
Não
|
|
| Códigos de linha
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Pulse Generator
|
Não
|
Não
|
| Scope
|
Sim
|
Sim
|
| Product
|
Sim
|
Sim
|
| Fcn
|
Não
|
Não
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Bernoulli Binary Generator
|
Não
|
Não
|
| Unipolar to Bipolar Converter
|
Não
|
Não
|
|
| DSP System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| ASpectrum Analyser
|
Sim
|
Sim
|
| Repeat
|
Sim
|
Sim
|
| Cumulative Sum
|
Não
|
Não
|
|
| Modulação por Amplitude de Pulso M-ária (PAM-M)
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Scope
|
Sim
|
Sim
|
| Display
|
Sim
|
Sim
|
| Complex to Real-Imag
|
Sim
|
Sim
|
| Sum
|
Sim
|
Sim
|
| Mux
|
Sim
|
Sim
|
| Goto
|
Sim
|
Sim
|
| From
|
Sim
|
Sim
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| M-PAM Modulator Baseband
|
Não
|
Não
|
| M-PAM Demodulator Baseband
|
Não
|
Não
|
| Error Rate Calculation
|
Sim
|
Sim
|
| Integer to Bit Converter
|
Não
|
Não
|
| Bit to Integer Converter
|
Não
|
Não
|
| Bernoulli Binary Generator
|
Não
|
Não
|
| Constellation Diagram
|
Sim
|
Sim
|
| Gaussian Noise Generator
|
Não
|
Não
|
|
| Transmissão digital em banda base
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Scope
|
Sim
|
Sim
|
| Discrete FIR Filter
|
Sim
|
Sim
|
| Sum, Add, Subtract, Sum of Elements
|
Sim
|
Sim
|
| Sine Wave
|
Sim
|
Sim
|
| Product
|
Sim
|
Sim
|
| Goto
|
Sim
|
Sim
|
| From
|
Sim
|
Sim
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| M-PAM Modulator Baseband
|
Não
|
Não
|
| M-PAM Demodulator Baseband
|
Não
|
Não
|
| Bernoulli Binary Generator
|
Não
|
Não
|
| Eye Diagram
|
Sim
|
Sim
|
| Gaussian Noise Generator
|
Não
|
Não
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Lowpass Filter
|
Não
|
Não
|
| Discrete Impulse
|
Não
|
Não
|
|
| Modulações digitais binárias
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Scope
|
Sim
|
Sim
|
| Sine Wave
|
Sim
|
Sim
|
| Switch
|
Sim
|
Sim
|
| Constant
|
Sim
|
Sim
|
| Product
|
Sim
|
Sim
|
| Goto
|
Sim
|
Sim
|
| From
|
Sim
|
Sim
|
| Sum
|
Sim
|
Sim
|
| Delay
|
Sim
|
Sim
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Windowed Integrator
|
Não
|
Não
|
| Integrate and Dump
|
Não
|
Não
|
| Bernoulli Binary Generator
|
Não
|
Não
|
|
| Modulações digitais M-árias
|
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Scope
|
Sim
|
Sim
|
| Complex to Real-Imag
|
Sim
|
Sim
|
| Display
|
Sim
|
Sim
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Random Integer Generator
|
Não
|
Não
|
| AWGN Channel
|
Não
|
Não
|
| Digital Baseband Modulation
|
Sim
|
Sim
|
| Constellation Diagram
|
Sim
|
Sim
|
| DSP System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Variance
|
Não
|
Não
|
|
| Transmissão digital em banda passante
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Goto
|
Sim
|
Sim
|
| Sum
|
Sim
|
Sim
|
| Display
|
Sim
|
Sim
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Random Integer Generator
|
Não
|
Não
|
| AWGN Channel
|
Não
|
Não
|
| QPSK Modulator Baseband
|
Sim
|
Sim
|
| QPSK Demodulator Baseband
|
Sim
|
Sim
|
| Constellation Diagram
|
Sim
|
Sim
|
| Eye Diagram
|
Sim
|
Sim
|
| Raised Cosine Transmit Filter
|
Sim
|
Sim
|
| DSP System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Spectrum Analyzer
|
Sim
|
Sim
|
| Subsistemas Subsystem
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Upconverter
|
Não
|
Não
|
| Interference
|
Não
|
Não
|
| Upconverted Spectra
|
Não
|
Não
|
| Downconverter
|
Não
|
Não
|
| Compute BER
|
Não
|
Não
|
| Calculate RMS EVM
|
Não
|
Não
|
|
| Multipath Fading Channel
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Bernoulli Binary Generator
|
Não
|
Não
|
| Digital Baseband Modulation
|
Sim (alguns blocos)
|
Sim (alguns blocos)
|
| Multipath Rayleigh Fading Channel
|
Não
|
Não
|
| Constellation Diagram
|
Sim
|
Sim
|
| Multipath Rician Fading Channel
|
Não
|
Não
|
|
| Digital Communications Ber Performance in AWGN or Fading
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Display
|
Sim
|
Sim
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Bernoulli Binary Generator
|
Não
|
Não
|
| Digital Baseband Modulation
|
Sim (alguns blocos)
|
Sim (alguns blocos)
|
| Multipath Rayleigh Fading Channel
|
Não
|
Não
|
| Constellation Diagram
|
Sim
|
Sim
|
| Multipath Rician Fading Channel
|
Não
|
Não
|
| AWGN Channel
|
Não
|
Não
|
| Eye Diagram
|
Sim
|
Sim
|
| Error Rate Calculation
|
Sim
|
Sim
|
|
| Orthogonal Frequency Multiplex Division (OFDM)
|
| Simulink
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Display
|
Sim
|
Sim
|
| Reshape
|
Sim
|
Sim
|
| Communications System Toolbox
|
Suporte HDL Coder no MATLAB 2014
|
Suporte HDL Coder no MATLAB 2015
|
| Random Integer Generator
|
Não
|
Não
|
| Digital Baseband Modulation
|
Sim (alguns blocos)
|
Sim (alguns blocos)
|
| Multipath Rayleigh Fading Channel
|
Não
|
Não
|
| Constellation Diagram
|
Sim
|
Sim
|
| Multipath Rician Fading Channel
|
Não
|
Não
|
| AWGN Channel
|
Não
|
Não
|
| Eye Diagram
|
Sim
|
Sim
|
| Error Rate Calculation
|
Sim
|
Sim
|
| OFDM Modulator Baseband
|
Não
|
Não
|
| OFDM Demodulator Baseband
|
Não
|
Não
|
|
Professor Orientador
Marcos Moecke
Aluno bolsista
Lucas Lucindo Vieira
Características da Bolsa
O projeto será financiado com bolsa PIBITI do CNPq e será executado entre Agosto de 2015 e Julho de 2015.