Mudanças entre as edições de "FIC MATLAB 2019-1"
(Criou página com '== Informações Básicas == :'''Código:''' MLB16470 :'''Professores:''' Diego da Silva de Medeiros :'''Início:''' :'''Término:''' :'''Horário:''' Terças e quinta...') |
|||
| (30 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 5: | Linha 5: | ||
:'''Professores:''' [[Diego da Silva de Medeiros]] | :'''Professores:''' [[Diego da Silva de Medeiros]] | ||
| − | :'''Início:''' | + | :'''Início:''' 12/03/2019 |
| − | :'''Término:''' | + | :'''Término:''' 23/05/2019 (feriados em 19 de março e 18 de abril) |
:'''Horário:''' Terças e quintas, das 19h às 22h | :'''Horário:''' Terças e quintas, das 19h às 22h | ||
| Linha 19: | Linha 19: | ||
== Conteúdos Abordados == | == Conteúdos Abordados == | ||
| − | === | + | === Apresentação da disciplina; Interface do MATLAB; Operadores; Funções; Constantes especiais; Formatos de exibição === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 1 - 12 de março}} |
* MATLAB e Octave; | * MATLAB e Octave; | ||
| Linha 161: | Linha 161: | ||
| − | * [[ | + | * [[FIC_MATLAB_2019-1/Aula-1|Códigos executados na aula]] |
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Vetores e matrizes === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 2 - 14 de março}} |
| Linha 207: | Linha 207: | ||
| − | * [[ | + | * [[FIC_MATLAB_2019-1/Aula-2|Códigos executados na aula]] |
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Operações com matrizes === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 3 - 21 de março}} |
* Operações; | * Operações; | ||
| Linha 293: | Linha 293: | ||
::Calcule ''x''. Em seguida, calcule <math>\sqrt{6x}</math>. ''Resposta: Aproximadamente <math>\pi</math>.'' | ::Calcule ''x''. Em seguida, calcule <math>\sqrt{6x}</math>. ''Resposta: Aproximadamente <math>\pi</math>.'' | ||
| + | |||
| + | * [[FIC_MATLAB_2019-1/Aula-3|Códigos executados na aula]] | ||
| + | |||
| + | {{collapse bottom}} | ||
| + | |||
| + | === Plots === | ||
| + | |||
| + | {{collapse top| bg=lightblue |Aula 4 - 26 de março}} | ||
* Plots: | * Plots: | ||
| Linha 377: | Linha 385: | ||
:* Comando ''close all'' para fechar todas figuras | :* Comando ''close all'' para fechar todas figuras | ||
| − | + | * '''Exercícios''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * '''Exercícios''' | ||
:1. Plote, em um mesmo gráfico, as funções | :1. Plote, em um mesmo gráfico, as funções | ||
| Linha 394: | Linha 393: | ||
::para <math>-2 \leq x \leq 2</math>. | ::para <math>-2 \leq x \leq 2</math>. | ||
| − | :2. Plote a função <math>\displaystyle{f(x) = x^2 + x - 2}</math> de -4 até 4 | + | :2. Plote a função <math>\displaystyle{f(x) = x^2 + x - 2}</math> de -4 até 4. Para certificar que o plot está correto, calcule na mão as raízes da função, e compare com os pontos onde a curva cruza o eixo horizontal (onde <math>\displaystyle{f(x) = 0}</math>) |
:3. Utilize o MATLAB para plotar a função <math>\displaystyle{T = 3 \ln (2 t) - 5 e^{0,5 t}}</math> ao longo do intervalo <math>1 \leq t \leq 3</math>. Insira um título na plotagem e rotule adequadamente os eixos. A variável ''T'' representa a temperatura em graus Celsius; a variável ''t'' representa o tempo em minutos. | :3. Utilize o MATLAB para plotar a função <math>\displaystyle{T = 3 \ln (2 t) - 5 e^{0,5 t}}</math> ao longo do intervalo <math>1 \leq t \leq 3</math>. Insira um título na plotagem e rotule adequadamente os eixos. A variável ''T'' representa a temperatura em graus Celsius; a variável ''t'' representa o tempo em minutos. | ||
| Linha 425: | Linha 424: | ||
[[Image:Exercícios Aula 3 FIC Matlab.jpg|600px|center]] | [[Image:Exercícios Aula 3 FIC Matlab.jpg|600px|center]] | ||
| + | :8. '''Desafio''': Resolva a questão 6, apresentando a resposta para um número genérico "N" de termos. | ||
| − | * [[ | + | |
| + | * [[FIC_MATLAB_2019-1/Aula-4|Gabarito]] | ||
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Endereçamento de vetores e matrizes === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 5 - 28 de março}} |
* Endereçamento de vetores e matrizes | * Endereçamento de vetores e matrizes | ||
| Linha 446: | Linha 447: | ||
| − | * [[ | + | * '''Exercícios:''' |
| + | |||
| + | :1. Crie uma matriz '''A''' de tamanho 15 x 15 de inteiros. | ||
| + | ::a) Extraia o elemento da segunda linha e quarta coluna de '''A''', armazenando na variável ''u'' | ||
| + | ::b) Crie um vetor '''v''' formado pelos elementos da segunda coluna de '''A''' | ||
| + | ::c) Crie um vetor '''w''' formado pelos elementos da última linha de '''A''' | ||
| + | ::d) Crie uma matriz '''B''' formada pelos elementos da segunda até a décima coluna de '''A''' | ||
| + | ::e) Crie uma matriz '''C''' formada pelos elementos da quinta até a penúltima linha de '''A''' | ||
| + | ::f) Crie uma matriz '''D''' formada pelos elementos da sétima até a penúltima linha e das 3 últimas colunas de '''A''' | ||
| + | ::g) Crie uma matriz '''E''' formada pelas linhas pares e colunas múltiplas de 3 de '''A''' | ||
| + | ::h) Crie uma matriz '''F''' formada pelas linhas 1 a 7 e mais a 13 e pelas colunas 4, 5 e 1 de '''A''' | ||
| + | |||
| + | :2. Assuma que a matriz '''C''' seja definida como abaixo e determine o conteúdo das seguintes submatrizes. Descubra a saída dos comandos antes de executá-los. | ||
| + | |||
| + | :::<math> | ||
| + | C = \begin{bmatrix} | ||
| + | 1{,}1 & -3{,}2 & 3{,}4 & 0{,}6 \\ | ||
| + | 0{,}6 & 1{,}1 & -0{,}6 & 3{,}1 \\ | ||
| + | 1{,}3 & 0{,}6 & 5{,}5 & 0{,}0 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |||
| + | ::a) C(2, :) | ||
| + | ::b) C(:, end) | ||
| + | ::c) C(1:2, 2:end) | ||
| + | ::d) C(6) | ||
| + | ::e) C(4:end) | ||
| + | ::f) C(1:2, 2:4) | ||
| + | ::g) C([1 3], 2) | ||
| + | ::h) C([2 2], [3 3]) | ||
| + | |||
| + | :3. Determine a saída no ''command window'' após a execução dos comandos abaixo. Descubra a saída dos comandos antes de executá-los. | ||
| + | |||
| + | ::: A = [1 2 3; 4 5 6; 7 8 9] | ||
| + | ::: A([3 1], :) = A([1 3], :) | ||
| + | ::: A([1 3], :) = A([2 2], :) | ||
| + | ::: A = A(:, [2 2]) | ||
| + | |||
| + | :4. Determine o conteúdo da matriz '''A''' após a execução das seguintes declarações. Descubra a saída dos comandos antes de executá-los. | ||
| + | |||
| + | ::a) A = eye(3,3); | ||
| + | ::: b = [1 2 3]; | ||
| + | ::: A(2, :) = b; | ||
| + | |||
| + | ::b) A = eye(3,3); | ||
| + | ::: b = [4 5 6]; | ||
| + | ::: A(:, 3) = b'; | ||
| + | |||
| + | ::c) A = eye(3,3); | ||
| + | ::: b = [7 8 9]; | ||
| + | ::: A(3, :) = b([3 1 2]); | ||
| + | |||
| + | |||
| + | * [[FIC_MATLAB_2019-1/Aula-5|Códigos executados na aula]] | ||
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Concatenação de matrizes; Texto; Entrada e saída de dados === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 6 - 02 de abril}} |
* Concatenação de vetores e matrizes | * Concatenação de vetores e matrizes | ||
* Comandos ''repmat'', ''reshape'', ''fliplr'' e ''flipud'' | * Comandos ''repmat'', ''reshape'', ''fliplr'' e ''flipud'' | ||
* Trabalhando com texto (''string'') | * Trabalhando com texto (''string'') | ||
| + | :* Conversão de dados (comandos ''double()'' e ''char()'') | ||
* Entrada/Saída de dados | * Entrada/Saída de dados | ||
| Linha 464: | Linha 519: | ||
:* Entrada de dados sem a tecla ENTER | :* Entrada de dados sem a tecla ENTER | ||
| + | |||
| + | * [[FIC_MATLAB_2019-1/Aula-6|Códigos executados na aula]] | ||
| + | |||
| + | {{collapse bottom}} | ||
| + | |||
| + | === Conjuntos; Polinômios; Números aleatórios; Aula de exercícios === | ||
| + | |||
| + | {{collapse top| bg=lightblue |Aula 7 - 04 de abril}} | ||
* '''Exercício''': | * '''Exercício''': | ||
| Linha 512: | Linha 575: | ||
:::::<math>\displaystyle{x^3 + 13x^2 + 52x + 6}</math> | :::::<math>\displaystyle{x^3 + 13x^2 + 52x + 6}</math> | ||
::ao longo da faixa <math>-7 \leq x \leq 1</math>. | ::ao longo da faixa <math>-7 \leq x \leq 1</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Linha 629: | Linha 631: | ||
:1. Plote um círculo com raio 2 e centrado no ponto (4,3). Dica: use equações paramétricas. | :1. Plote um círculo com raio 2 e centrado no ponto (4,3). Dica: use equações paramétricas. | ||
:2. Repita o Exercício 6 da Aula 4 com um número genérico de termos <math>\sin()</math> somados em <math>g(x)</math>. | :2. Repita o Exercício 6 da Aula 4 com um número genérico de termos <math>\sin()</math> somados em <math>g(x)</math>. | ||
| − | :3. Plote o símbolo do | + | :3. Plote o símbolo do Bátma (para quem tem dúvida, [http://guangchuangyu.github.io/blog_images/2011/08/X.png link]). |
| − | * [[ | + | * [[FIC_MATLAB_2019-1/Aula-7|Códigos executados na aula]] |
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Variáveis lógicas; Operadores relacionais e lógicos === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 8 - 09 de abril}} |
* Variáveis lógicas (''booleanas''): | * Variáveis lógicas (''booleanas''): | ||
| Linha 690: | Linha 692: | ||
* Comando ''find'' | * Comando ''find'' | ||
| + | :* Localizar e substituir | ||
| Linha 727: | Linha 730: | ||
::b) A temperatura em São José se encontra entre 1 °C e 15 °C (incluindo ambos os extremos). | ::b) A temperatura em São José se encontra entre 1 °C e 15 °C (incluindo ambos os extremos). | ||
::c) Fez mais frio na Palhoça que em São José. | ::c) Fez mais frio na Palhoça que em São José. | ||
| − | ::d) Biguaçu | + | ::d) Biguaçu alcança temperaturas mais altas. |
:3. A altura e a velocidade de um projétil lançado com uma velocidade <math>v_0</math> e um ângulo com a horizontal <math>a</math> são dadas, em funcão do tempo ''t'', por | :3. A altura e a velocidade de um projétil lançado com uma velocidade <math>v_0</math> e um ângulo com a horizontal <math>a</math> são dadas, em funcão do tempo ''t'', por | ||
| Linha 739: | Linha 742: | ||
::e) Destaque as figuras anteriores com os intervalos calculados na letra c). | ::e) Destaque as figuras anteriores com os intervalos calculados na letra c). | ||
| − | * [[ | + | * [[FIC_MATLAB_2019-1/Aula-8|Códigos executados em sala]] |
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Controle de fluxo de dados - ''if'' e ''switch'' === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 9 - 11 de abril}} |
* Uso de scripts: | * Uso de scripts: | ||
| Linha 791: | Linha 794: | ||
| − | * [[ | + | * [[FIC_MATLAB_2019-1/Aula-9|Códigos executados em sala]] |
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Struct e Cell === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 10 - 16 de abril}} |
* Estruturas | * Estruturas | ||
| Linha 880: | Linha 883: | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* Arranjo de células: texto e números | * Arranjo de células: texto e números | ||
| Linha 898: | Linha 893: | ||
| − | + | * [[FIC_MATLAB_2019-1/Aula-10|Códigos executados em sala]] | |
| − | * [[ | ||
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Estruturas de repetição - ''for'' e ''while'' === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 11 - 23 de abril}} |
* Estruturas de repetição: | * Estruturas de repetição: | ||
| Linha 971: | Linha 965: | ||
| − | * [[ | + | * [[FIC_MATLAB_2019-1/Aula-11|Códigos executados em sala]] |
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Funções === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 12 - 25 de abril}} |
* Funções definidas pelo usuário | * Funções definidas pelo usuário | ||
| Linha 1 006: | Linha 1 000: | ||
| − | * [[ | + | * [[FIC_MATLAB_2019-1/Aula-12|Códigos executados em sala]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Interface gráfica === |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{collapse top| bg=lightblue |Aula 13 - 30 de abril}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {{collapse top| bg=lightblue | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Curso Matlab aplicado ao processamento de imagens - Aula 2|Aula]] | [[Curso Matlab aplicado ao processamento de imagens - Aula 2|Aula]] | ||
| Linha 1 402: | Linha 1 177: | ||
{{collapse bottom}} | {{collapse bottom}} | ||
| − | [[ | + | [[FIC_MATLAB_2019-1/Aula-13|Códigos executados em sala]] |
| + | |||
| + | {{collapse bottom}} | ||
| + | |||
| + | === Processamento de imagens === | ||
| + | |||
| + | {{collapse top| bg=lightblue |Aula 14 - 02 de maio}} | ||
| + | |||
| + | <!--'''Pro futuro:''' Usar ''im2double''!--> | ||
| + | |||
| + | [[Curso Matlab aplicado ao processamento de imagens - Aula 3]] | ||
| + | |||
| + | |||
| + | * [[FIC_MATLAB_2019-1/Aula-14|Códigos executados na aula]] | ||
| + | |||
| + | {{collapse bottom}} | ||
| + | |||
| + | === Solução de sistemas de equações; Toolbox simbólico === | ||
| + | |||
| + | {{collapse top| bg=lightblue |Aula 15 - 07 de maio}} | ||
| + | |||
| + | * Sistemas de equações lineares | ||
| + | :* Encontrando a solução de ''Ax = b'' com ''A\b'' | ||
| + | <!-- Talvez falar sobre a função rref - forma escalonada reduzida de linha --> | ||
| + | ::* Exemplo: Balanceamento de equações químicas | ||
| + | |||
| + | :::::<math>C_3 H_8 + O_2 ~~~ \longrightarrow ~~~ CO_2 + H_2 O</math> | ||
| + | |||
| + | :::::<math>x (C_3 H_8) + y (O_2) ~~~ \longrightarrow ~~~ z (C O_2) + w (H_2 O)</math> | ||
| + | |||
| + | :::::<math>\begin{cases} | ||
| + | 3x = z & \text{(carbono)} \\ | ||
| + | 8x = 2w & \text{(hidrogenio)} \\ | ||
| + | 2y = 2z + w & \text{(oxigenio)} \\ | ||
| + | x + y + z + w = 1 & \text{(normalizacao)} \\ | ||
| + | \end{cases}</math> | ||
| + | |||
| + | :::::<math>\begin{cases} | ||
| + | 3x - z = 0 \\ | ||
| + | 8x - 2w = 0 \\ | ||
| + | 2y - 2z - w = 0 \\ | ||
| + | x + y + z + w = 1 \\ | ||
| + | \end{cases}</math> | ||
| + | |||
| + | <!-- [[Image:MATLAB_Chem_Balance.jpg|300px|center]] --> | ||
| + | |||
| + | |||
| + | * Toolbox simbólico | ||
| + | |||
| + | :* Básico | ||
| + | |||
| + | ::* Comandos ''syms'' e ''sym'' | ||
| + | ::* Comandos ''pretty'' e ''latex'' | ||
| + | ::* Comando ''subs'' | ||
| + | :::* Valores via argumento da função | ||
| + | :::* Valores retirados do workspace | ||
| + | ::* Comandos ''factor'', ''expand'', ''collect'' e ''simplify'' | ||
| + | |||
| + | :* Cálculo | ||
| + | |||
| + | ::* Comando ''limit'': Limites | ||
| + | :::* <math>\lim_{x \to 0} \frac{\sin(x)}{x}</math> | ||
| + | :::* <math>\lim_{x \to \infty} \left( 1 + \frac{1}{x} \right)^x</math> | ||
| + | ::* Comando ''diff'': Derivada primeira, segunda, terceira, etc. | ||
| + | ::* Comando ''int'': Integrais indefinidas e definidas | ||
| + | :::* <math>\int x^a dx</math> | ||
| + | |||
| + | :* Interlúdio: comandos ''assume'' e ''assumptions'' | ||
| + | |||
| + | :* Mais cálculo | ||
| + | |||
| + | ::* Comando ''taylor'': Séries de Taylor | ||
| + | ::* Comando ''symsum'': Somatórios / séries | ||
| + | ::* Outros: ''dsolve'', ''fourier'', ''laplace'', ''partfrac'' | ||
| + | |||
| + | :* Solução de equações | ||
| + | ::* Comando ''solve'' | ||
| + | |||
| + | |||
| + | [[FIC_MATLAB_2019-1/Aula-15|Códigos executados em sala]] | ||
| + | |||
| + | {{collapse bottom}} | ||
| + | |||
| + | === Importação de dados; Gráficos em 2D e 3D === | ||
| + | |||
| + | {{collapse top| bg=lightblue |Aula 16 - 09 de maio}} | ||
| + | |||
| + | * Importação de dados | ||
| + | :* Comando ''uiimport'' | ||
| + | :* Formato do separador decimal (''.'' ou '','') | ||
| + | |||
| + | : Exemplo: usar [https://wiki.sj.ifsc.edu.br/images/8/84/Celular4g.txt Celular4g.txt], importar e trabalhar com as funções de matrizes. | ||
| + | |||
| + | |||
| + | *'''Exercícios''': | ||
| + | |||
| + | :1. Com o arquivo [https://wiki.sj.ifsc.edu.br/images/f/fe/Add_user.txt Add_user.txt] (Adições Líquidas de Aparelhos 4G das Operadoras no período), calcular a soma dos anos 2014, 2015 e 2016 (até o momento) por operadora e a soma e a média por período. | ||
| + | |||
| + | |||
| + | * '''Gráficos em 2D''' | ||
| + | |||
| + | :* Revisão: Comandos ''plot'', ''stem'', ''bars'' e ''stairs'' | ||
| + | |||
| + | :* Comandos ''semilogx'', ''semilogy'' e ''loglog'' | ||
| + | |||
| + | ::* Exemplo: Resposta em frequência de um [https://en.wikipedia.org/wiki/Low-pass_filter filtro passa-baixa] de segunda ordem: | ||
| + | |||
| + | :::<math>H(\omega) = \dfrac{1}{\sqrt{1 + \omega^2}}</math> | ||
| + | |||
| + | :* Comando ''polar'' | ||
| + | |||
| + | ::* Exemplo: [https://pt.wikipedia.org/wiki/Rosa_polar Rosas polares]: | ||
| + | ::: <math>\rho = \mathrm{cos}(k \theta)</math>, onde ''k'' é um parâmetro. | ||
| + | |||
| + | ::* Números complexos e funções ''abs'' e ''angle'' | ||
| + | |||
| + | :* Comando ''plotyy'' para plotar gráficos com dois eixos em '''y'''. | ||
| + | |||
| + | :* Letras gregas nos gráficos: | ||
| + | :::{| class="wikitable" | ||
| + | ! '''Letra''' | ||
| + | ! '''Representação''' | ||
| + | |- | ||
| + | | <math> \alpha </math> || \alpha | ||
| + | |- | ||
| + | | <math> \beta </math> || \beta | ||
| + | |- | ||
| + | | <math> \gamma </math> || \gamma | ||
| + | |- | ||
| + | | <math> \delta </math> || \delta | ||
| + | |- | ||
| + | | <math> \epsilon </math> || \epsilon | ||
| + | |- | ||
| + | | <math> \kappa </math> || \kappa | ||
| + | |- | ||
| + | | <math> \lambda </math> || \lambda | ||
| + | |- | ||
| + | | <math> \mu </math> || \mu | ||
| + | |- | ||
| + | | <math> \nu </math> || \nu | ||
| + | |- | ||
| + | | <math> \omega </math> || \omega | ||
| + | |- | ||
| + | | <math> \phi </math> || \phi | ||
| + | |- | ||
| + | | <math> \pi </math> || \pi | ||
| + | |- | ||
| + | | <math> \chi </math> || \chi | ||
| + | |- | ||
| + | | <math> \psi </math> || \psi | ||
| + | |- | ||
| + | | <math> \rho </math> || \rho | ||
| + | |- | ||
| + | | <math> \sigma </math> || \sigma | ||
| + | |- | ||
| + | | <math> \tau </math> || \tau | ||
| + | |- | ||
| + | | <math> \upsilon </math> || \upsilon | ||
| + | |- | ||
| + | | <math> \Sigma </math> || \Sigma | ||
| + | |- | ||
| + | | <math> \Pi </math> || \Pi | ||
| + | |- | ||
| + | | <math> \Lambda </math> || \Lambda | ||
| + | |- | ||
| + | | <math> \Omega </math> || \Omega | ||
| + | |- | ||
| + | | <math> \Gamma </math> || \Gamma | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | <!-- | ||
| + | Exercício (livro - adaptado - 10 p.253): Muitas aplicações utilizam a seguinte aproximação de "ângulo pequeno" para o seno com a finalidade de se obter um modelo mais simples que seja fácil de ser entendido e analisado. A aproximação estabelece que ''sen(x)'' <math>\simeq x</math>, em que ''x'' deve ser em radianos. Investigue a precisão desta aproximação com dois plots. No primeiro, plote ''sen(x) versus x'' para <math>0 \leq x \leq 1</math>. No segundo, plote o erro da aproximação ''(sen(x) - x) versus x'' para <math>0 \leq x \leq 1</math>. | ||
| + | --> | ||
| + | |||
| + | * '''Exercícios''': | ||
| + | |||
| + | :1. Plote '''em vermelho''' a função polar | ||
| + | :::<math>\rho = \dfrac{\mathrm{sen}(\theta) \sqrt{|\cos(\theta)|}} {\mathrm{sen}(\theta) + 7/5} - 2 \mathrm{sen}(\theta) + 2</math>, de <math>-\pi \leq \theta \leq \pi</math>. | ||
| + | |||
| + | :2. Plote o gráfico da função <math>\sqrt{x}</math> utilizando todos os quatro tipos de combinações de eixos (linear/logarítmico). | ||
| + | |||
| + | :3. As seguintes funções descrevem as oscilações em circuitos elétricos e as vibrações de máquinas e estruturas. Sobreponha as plotagens dessas funções no mesmo eixo. Como elas são similares, defina qual é a melhor forma de plotá-las e de rotulá-las para evitar confusão. | ||
| + | ::: <math>\displaystyle{x(t) = 1000 e^{-0,5t} \mathrm{sen}(3t+2)}</math> | ||
| + | ::: <math>\displaystyle{y(t) = 7 e^{-0,4t} \cos(5t-3)}</math> | ||
| + | |||
| + | |||
| + | * '''Gráficos em 3D''' | ||
| + | |||
| + | :* Gráficos de linha em 3D | ||
| + | ::* Comando ''plot3'' | ||
| + | |||
| + | :::* Exemplo: Equações paramétricas para uma [https://pt.wikipedia.org/wiki/H%C3%A9lice_(geometria) hélice circular]: | ||
| + | ::::: <math>x = a \cos(t)</math> | ||
| + | ::::: <math>y = a \sin(t)</math> | ||
| + | ::::: <math>z = b t </math> | ||
| + | |||
| + | ::* Comando ''view'' | ||
| + | ::* Rótulo no eixo z: ''zlabel'' | ||
| + | |||
| + | :* Gráficos de superfície | ||
| + | ::* Comando ''meshgrid'' para criar uma malha 3D | ||
| + | ::* Comando ''surf'' para plot de função de ''f(x,y)'' | ||
| + | :::* Comando ''shading'', com parâmetros ''flat'', ''faceted'' e ''interp'' | ||
| + | :::* Comando alternativo ''mesh'' | ||
| + | |||
| + | :::* Exemplo: Símbolo da Itapema FM incompleto: | ||
| + | ::::: [X,Y] = meshgrid(-20:0.5:20); | ||
| + | ::::: R = sqrt(X.^2 + Y.^2) + eps; | ||
| + | ::::: Z = sin(R)./R; | ||
| + | ::::: surf(X,Y,Z) | ||
| + | |||
| + | :* Curva de níveis: | ||
| + | |||
| + | ::* Comandos ''contour'', ''surfc'' e ''meshc'' | ||
| + | |||
| + | |||
| + | * [[Media:FIC_Matlab_Exercicios_plot.pdf|Exercícios]] | ||
| + | |||
| + | * [[FIC_MATLAB_2019-1/Aula-16|Códigos executados em sala]] | ||
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Projeto === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 17 - 14 de maio}} |
Aula dedicada ao projeto. | Aula dedicada ao projeto. | ||
| Linha 1 414: | Linha 1 408: | ||
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Projeto === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 18 - 16 de maio}} |
Aula dedicada ao projeto. | Aula dedicada ao projeto. | ||
| Linha 1 422: | Linha 1 416: | ||
{{collapse bottom}} | {{collapse bottom}} | ||
| − | === | + | === Projeto === |
| − | {{collapse top| bg=lightblue | | + | {{collapse top| bg=lightblue |Aula 19 - 21 de maio}} |
Aula dedicada ao projeto. | Aula dedicada ao projeto. | ||
| Linha 1 455: | Linha 1 449: | ||
:esteganografia | :esteganografia | ||
:batalha naval | :batalha naval | ||
| + | :campo minado | ||
| + | :dominar o mundo | ||
Edição atual tal como às 20h11min de 19 de setembro de 2019
Informações Básicas
- Código: MLB16470
- Professores: Diego da Silva de Medeiros
- Início: 12/03/2019
- Término: 23/05/2019 (feriados em 19 de março e 18 de abril)
- Horário: Terças e quintas, das 19h às 22h
- Referência Básica: PALM, William J. Introdução ao MATLAB para engenheiros. Tradução de Tales Argolo Jesus. 3. ed. Porto Alegre: AMGH, 2013. xiv, 562, il. ISBN 9788580552041
- Referência Complementar: MORAIS, V.. VIEIRA, C. MATLAB Curso Completo. FCA, 2013. 644. ISBN 9727227058
Conteúdos Abordados
Apresentação da disciplina; Interface do MATLAB; Operadores; Funções; Constantes especiais; Formatos de exibição
| Aula 1 - 12 de março | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Observações:
|
Vetores e matrizes
| Aula 2 - 14 de março |
|---|
|
|
Operações com matrizes
| Aula 3 - 21 de março |
|---|
|
Plots
| Aula 4 - 26 de março | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Endereçamento de vetores e matrizes
| Aula 5 - 28 de março |
|---|
|
Concatenação de matrizes; Texto; Entrada e saída de dados
| Aula 6 - 02 de abril |
|---|
|
Conjuntos; Polinômios; Números aleatórios; Aula de exercícios
| Aula 7 - 04 de abril | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Variáveis lógicas; Operadores relacionais e lógicos
| Aula 8 - 09 de abril | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Controle de fluxo de dados - if e switch
| Aula 9 - 11 de abril |
|---|
|
Struct e Cell
| Aula 10 - 16 de abril | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Estruturas de repetição - for e while
| Aula 11 - 23 de abril | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Funções
| Aula 12 - 25 de abril |
|---|
|
Interface gráfica
| Aula 13 - 30 de abril | ||
|---|---|---|
|
Processamento de imagens
| Aula 14 - 02 de maio |
|---|
|
|
Solução de sistemas de equações; Toolbox simbólico
| Aula 15 - 07 de maio |
|---|
|
Importação de dados; Gráficos em 2D e 3D
| Aula 16 - 09 de maio | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Projeto
| Aula 17 - 14 de maio |
|---|
|
Aula dedicada ao projeto. |
Projeto
| Aula 18 - 16 de maio |
|---|
|
Aula dedicada ao projeto. |
Projeto
| Aula 19 - 21 de maio |
|---|
|
Aula dedicada ao projeto. |
Questões da turma
Projetos finais
Ideias
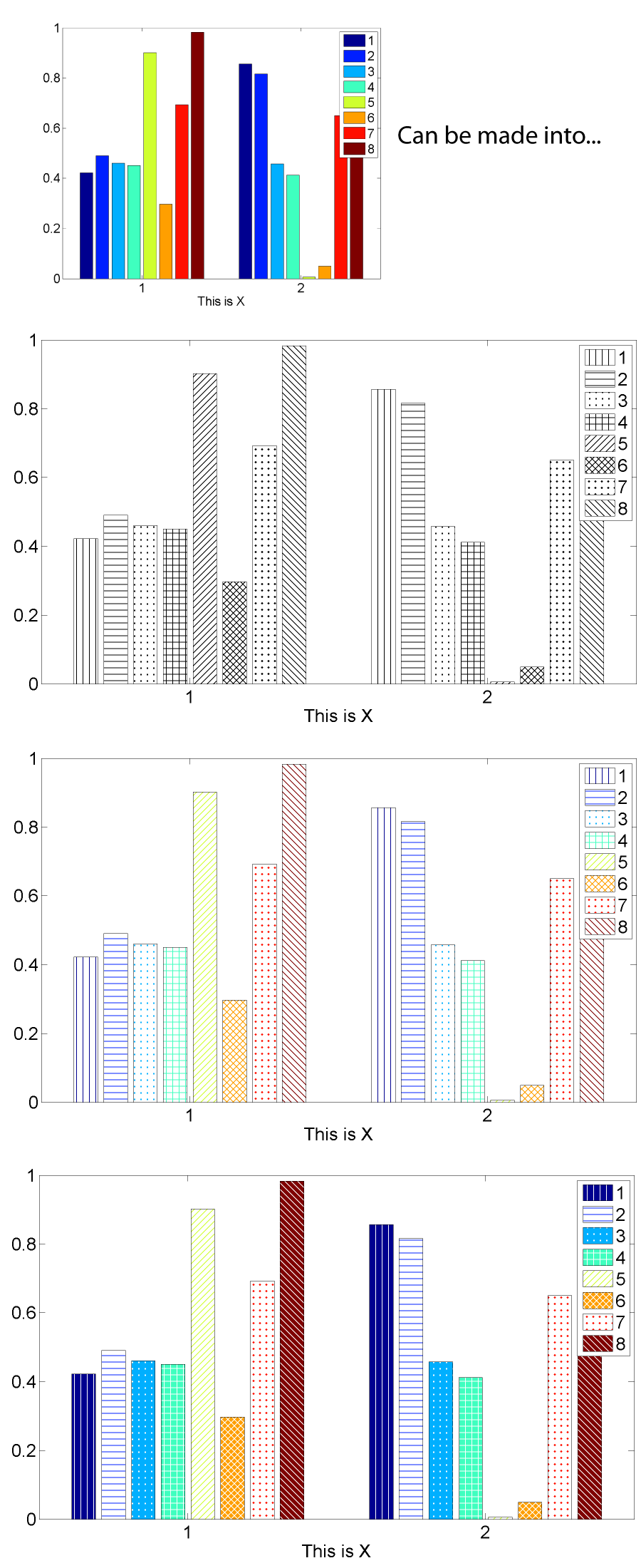
Hachuras em gráficos de barras
Implementar uma função em MATLAB que plote um gráfico de barras com hachuras. O comportamento deve ser semelhante ao comando bar, nativo do MATLAB, mas parâmetros poderão ser acrescentados para controle da trama. Um exemplo de resultado pode ser visto na figura abaixo:
Genius®
Implementar uma versão avançada do jogo Genius® construído na aula 9, adicionando sons, elementos gráficos, etc.
Outros
- relógio analógico
- dtmf
- sudoku
- jogo da velha
- contar moedas
- esteganografia
- batalha naval
- campo minado
- dominar o mundo