FIC MATLAB 2016-2

Prof. Bruno William Wisintainer e-mail

Informações Básicas

Início: 11/Ago/2016
Término: 18/Out/2016
Referência Básica: PALM, William J. Introdução ao MATLAB para engenheiros. Tradução de Tales Argolo Jesus. 3. ed. Porto Alegre: AMGH, 2013. xiv, 562, il. ISBN 9788580552041
Referência Complementar: MORAIS, V.. VIEIRA, C. MATLAB Curso Completo. FCA, 2013. 644. ISBN 9727227058

Conteúdos Abordados

Aula 1

11/Ago

- Janela de comandos; - Inserindo comandos na Command Window; - Variável ans; - Ordem de precedência: Símbolo Operação Forma no Matlab ^ Exponenciação: $a^{b}$ a^b * Multiplicação: $ab$ a*b / Divisão à direita: ${\frac {a}{b}}$ a/b \ Divisão à esquerda: ${\frac {b}{a}}$ a\b + Adição: $a+b$ a+b - Subtração: $a-b$ a-b - Lista de Exercícios: - Exemplos de help e lookfor; - Usando o arquivo m (m file); - Comando clear all para apagar todas variáveis; - Comando clc para apagar texto na Command Window; - Definições de vetores; - Definições de matrizes; - Definições de matrizes eye, zeros e ones; - Transposição de vetor ou matriz com o apóstrofo ( ' ); - Resolução de sistema linear: ${\begin{alignedat}{7}2x&\;-&\;3y&\;-&\;{\sqrt {2}}z&\;=&\;3,643\\2,3x&\;+&\;\pi y&\;+&\;{\sqrt[{3}]{35}}z&\;=&\;54,181\\\pi x&\;+&\;{\rm {e}}^{1}y&\;+&\;2,9z&\;=&\;64,0368\end{alignedat}}$ - Representação de números complexos. - Variáveis e constantes especiais: - Utilização do ponto e vírgula (;) para não aparecer na Command Window; - Contador de tempo tic e toc; - Variáveis constantes e especiais: Comandos Descrições ans Variável temporária que contém a resposta mais recente. eps Verifica a acurácia da precisão do ponto flutuante. i,j A unidade imaginária ${\sqrt {-1}}$. Inf Infinito. NaN Indica um resultado numérico indefinido. pi O número $\pi$.

Aula 2

16/Ago

- Formatos de exibição Comando Descrição e exemplo format short Quatro dígitos decimais (padrão); 13.6745 format long 16 dígitos; 17.27484029463547 format short e Cinco dígitos (quatro decimais) mais o expoente; 6.3792e+03 format long e 16 dígitos (15 decimais) mais o expoente; 6.379243784781294e-04 format bank Dois dígitos decimais; 126.73 format + Positivo, negativo ou zero; + format rat Aproximação racional; 43/7 format compact Suprime algumas linhas em branco format loose Restabelece o modo de exibição menos compacto - Funções Matemáticas Função Sintaxe no Matlab $e^{x}$ exp(x) ${\sqrt {x}}$ sqrt(x) ln x log(x) $\log _{10}x$ log10(x) cos x cos(x) sen x sin(x) tan x tan(x) cos-1x acos(x) sen-1x asin(x) tan-1x atan(x) utilizando d após as funções sin, cos e tan e suas inversas, faz o cálculo em graus - Arranjo de vetor utilizando dois pontos (:); - Definição de passo; - Comando plot de uma função; - Comando hold on para manter a curva no gráfico; - Comando grid on para mostrar linhas em forma de grade; - Nomes aos eixos com xlabel e ylabel - Comando close all para fechar todas figuras; - Exercício: Plotar a função $f(x)=x^{2}+x-2$ de -4 até 4 e encontrar as raízes por Bhaskara - Raízes de um vetor usando comando roots; - Comando length;

Aula 3

18/Ago

Exercício: Fazer o plot de um sinal de tensão x tempo, como da figura abaixo: de $t=1s$ até $t=63s$ → função seno de $t=64s$ até $t=80s$ → 0 de $t=81s$ até $t=100s$ → 1 de $t=101s$ até $t=120s$ → -1 Não esquecer de nomear os eixos. - Comando axis. - Comando size; - Endereçamento de matrizes; - Exclusão de linha ou coluna; - Comando sort; - Comando find; - Comando sum; - Criação de vetor igualmente espaçamento: linear (linspace) e logarítmico (logspace); - Norma (norm) e módulo (abs) de um vetor.

Aula 4

23/Ago

Exercício (livro - 16 p. 101): A tabela a seguir mostra o salário por hora, as horas de trabalho e a produção (número de dispositivos produzidos) em uma semana para cinco fabricantes de dispositivos. Trabalhador 1 Trabalhador 2 Trabalhador 3 Trabalhador 4 Trabalhador 5 Salário por hora ($) 5 5,50 6,50 6 6,25 Horas de trabalho 40 43 37 50 45 Produção (dispositivos 1000 1100 1000 1200 1100 Utilize o MATLAB para responder essas questões: a) Quanto cada trabalhador lucrou na semana? b) Qual foi o salário total pago? c) Quantos dispositivos foram fabricados? d) Qual é o custo médio para se produzir um dispositivo? e) Quantas horas são necessárias, em média, para se produzir um dispositivo? f) Assumindo que a produção de cada trabalhador tenha a mesma qualidade, qual trabalhador é o mais eficiente? Qual é o menos eficiente? - Comandos mean, ceil, floor e round; Exercício: A corda da figura abaixo está presa nos pontos A e B, determine seu comprimento e a sua direção, medidos de A para B. 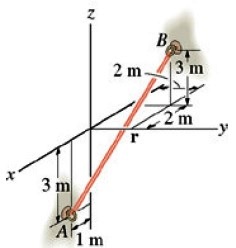- Produto escalar (dot) e produto vetorial (cross) de dois vetores; Exercício: Calcule o produto vetorial e escalar dos vetores: ${\overrightarrow {a}}=2{\overrightarrow {i}}+3{\overrightarrow {j}}-2{\overrightarrow {k}}$, ${\overrightarrow {b}}=-3{\overrightarrow {i}}-5{\overrightarrow {k}}$ - Comando poly para criar um polinômio a partir de raízes; - Comparação com comando roots; - Multiplicação de polinômios (conv); - Divisão de polinômios (deconv), com ou ser resto; - Plot de um polinômio a partir de um intervalo de pontos. (polyval)

Aula 5

25/Ago

- Comando input para entrada de dados; - Comando disp para mostrar mensagem; Exercício: Criar uma calculadora de IMC com perguntas (input) para massa e altura, aparecendo na sequência o resultado - Criando estruturas; - Criando estruturas com o comando struct; - Comando rmfield para remover campo da estrutura; - Comando isfield para identificar se um campo existe ou não; - Arranjo de células: texto e números; - Comando celldisp e cellplot; - Cálculo de determinante de uma matriz (det).

Aula 6

30/Ago

- Funções trigonométricas; - Funções hiperbólicas; - Função definida pelo usuário no arquivo .m; Exercício: Criar uma função no arquivo .m da definição pelo exponencial do cosseno hiperbólico e do seno hiperbólico, comparando com a funções já existentes (cosh e sinh), plotar as curvas idênticas em 2 figuras (arquivo .m 1). Criar um novo arquivo .m com valores de entrada de $-\pi$ até $\pi$ (arquivo .m 2). - Importar arquivo para o Matlab, pelo menu e pelo comando uiimport; Exemplo: usar [Celular4g‎.txt], importar e trabalhar com as funções de matrizes. - Padronizar para o formato que o Matlab reconhece os números: ponto (.) e (,); - Converter formato table2array. - Comando subplot.

Aula 7

01/Set

Exercício: com o arquivo [Add_user.txt] (Adições Líquidas de Aparelhos 4G das Operadoras no período), calcular a soma dos anos 2014, 2015 e 2016 (até o momento) por operadora e a soma e a média por período. - Tipos de códigos: Sequenciais, Condicionais e Iterativos; Operadores relacionais Operador relacional Significado < Menor que <= Menor ou igual a > Maior que >= Maior ou igual a == Igual a ~= Não é igual a Operadores de curto circuito Operador Nome && E $||$ OU - As sentenças if, else e elseif. Exercício: Criar um código que calcula o valor total da compra de algumas unidades de arroz (5kg), feijão (1kg) e café (500g). O preço unitário do arroz é R$15,00. Se comprar 3 o preço cai para R$14,00 cada. O preço unitário do feijão é R$12,00. Se comprar 4 o preço cai para R$11,50 cada. O preço unitário do café é R$10,00. Se comprar 3 o preço cai para R$9,25 cada. Colocar opção de entrada de dados com input e condição que não existe unidade negativa. - Laços for.

Aula 8

06/Set

Exercício: Calcule e armazene a Sequência de Fibonacci, com a possibilidade de escolher o número de termos. Exercício: Criar uma matriz (NxN) em que a diagonal principal é o produto de linha por coluna e nos outros termos é a soma da linha com a coluna, com a possibilidade de escolher a dimensão N da matriz. Exercício: Calcule o fatorial de um número que pode ser escolhido. - Laços while. Exercício (livro - Exemplo 4.6-2 p. 186): Determine o tempo necessário para que você acumule pelo menos $10000 em uma conta bancária se você depositar inicialmente $500 e mais $500 ao final de cada ano, com um rendimento anual de 5%. Exercício: Fazer o plot de um sinal de tensão x tempo, como da figura abaixo, usando os conceitos da aula de hoje: de $t=1s$ até $t=63s$ → função seno de $t=64s$ até $t=80s$ → 0 de $t=81s$ até $t=100s$ → 1 de $t=101s$ até $t=120s$ → -1 Não esquecer de nomear os eixos.

Aula 9

08/Set

- A estrutura switch. Exercício (livro - adaptado - T4.7-1 p. 189): Complemente o exercício anterior (resolvido em sala, exemplo p. 189) com os ângulos 0, 90, 180, 270 e 360 e as coordenadas. Exercício (livro - Exemplo 4.7-1 p. 189): Utilize a estrutura switch para calcular o total de dias decorridos em um ano. Entrada de dados: o número do mês (1 até 12), o dia e a indicação de o ano ser bissexto ou não. Exercício: Usando switch, calcule a soma dos ângulos internos de uma figura geométrica. Entrada de dados: o nome da figura, pelo menos até o hexágono.

Aula 10

13/Set

Exercício (livro - adaptado - 43 p. 215): Utilize a estrutura switch para calcular a quantidade de dinheiro que é acumulada em uma conta durante um ano. O programa deve aceitar as seguintes entradas: a quantidade inicial de dinheiro depositada na conta; a frequência do rendimento (mensal, trimestral, semestral ou anual); e o rendimento. Rode o seu programa para um depósito inicial que pode ser escolhido (por exemplo R$1000); utilize um rendimento a sua escolha (por exemplo 5%). - Tipos de axis: Escala automática, equal, square e definido manualmente; - Comando title; - Plot de número complexo; - Comando fplot e comparação com plot; Exercício (livro - T5.1-2 p. 224): Utilize o comando fplot para investigar a função $tan(cos(x))-sen(tan(x))$ para $0\leq x\leq 2\pi$. Quantos valores de $x$ aproximadamente são necessários para que seja obtida a mesma plotagem utilizando-se o comando plot? - Comando legend; - Especificadores de linha, cores e marcadores: Tipo de linha Símbolo Sólida (padrão) - Tracejada -- Tracejada com pontos -. Com pontos : Cores Símbolo Preto k Azul b Ciano c Verde g Magenta m Vermelho r Branco w Amarelo y Marcadores de dados Símbolo Ponto . Asterisco * Cruz x Círculo o Adição + Quadrado s Losango d Triângulo apontando pra cima ^ Triângulo apontando pra baixo v Triângulo apontando pra direita > Triângulo apontando pra esquerda < Estrela de 5 pontas p Estrela de 6 pontas h

Aula 11

15/Set

Exercício (livro): Plote a parte imaginária versus a parte real da função $(0,2+8i)$n para $0\leq n\leq 20$. Escolha uma quantidade suficiente de pontos para obter uma curva suave. Rotule cada eixo e insira um título. Utilize o comando axis para alterar o espaçamento entro os rótulos dos tick-marks. Exercício (1 - livro adaptado): A análise de equilíbrio determina o volume de produção para qual o qual o custo de produção total é igual à receita total. No ponto de equilíbrio, não há lucro nem perda. Em geral, os custos da produção consistem em custos fixos e custos variáveis. Os custos fixos incluem salários daqueles não diretamente envolvidos com a produção, custos de manutenção de fábrica, seguros, e assim por diante. Os custos variáveis dependem do volume de produção e incluem custos de material, trabalho e energia. Na análise a seguir, considere que nós produzimos apenas o que podemos vender; assim, a quantidade de produção é igual à quantidade de vendas. Q é a quantidade de produção, em galões por ano. Considere os seguintes custos para um determinado produto químico: - Custo fixo: $10 mil por ano. - Custo variável: 25 centavos por galão de produto. - O preço de venda é de 65 centavos por galão. Utilize esses dados para plotar o custo total e a receita versus Q, e determine graficamente o ponto de equilíbrio. Para qual faixa de Q a produção gera lucro? - Comandos gtext para colocar texto na figura com um clique e text para colocar texto em uma coordenada definida.

Aula 12

20/Set

- Comparação de gráficos: plot, loglog, semilogx e semilogy; Exercício (livro - T5.2-1 p. 228): Escolha um espaçamento adequado para t e v, e utilize o comando subplot para plotar a função $x=e$-0,5t$cos(20t-6)$ para $0\leq t\leq 8$ e a função $u=6\log _{10}(v$2$+20)$ para $-8\leq v\leq 8$. Rotule cada eixo. Utilize os comandos semilogx, semilogy ou loglog. 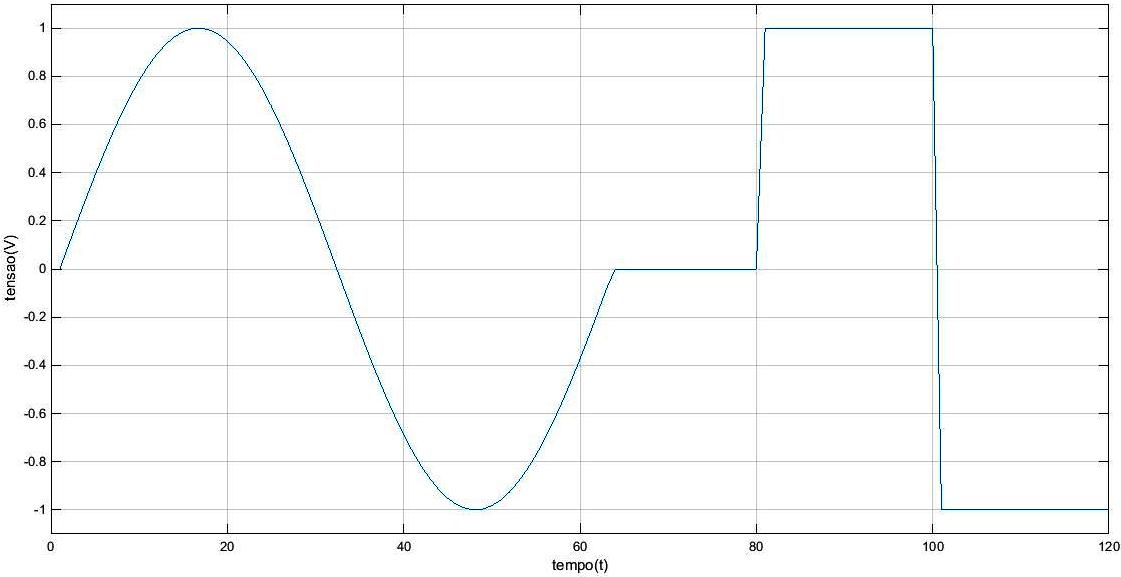- Gráfico com dois eixos em y (plotyy); Exercício (livro - adaptado - 15 p. 254): As seguintes funções descrevem as oscilações em circuitos elétricos e as vibrações de máquinas e estruturas. Sobreponha as plotagens dessas funções no mesmo eixo. Como elas são similares, defina qual é a melhor forma de plotá-las e de rotulá-las para evitar confusão. $x(t)=10e$-0,5t$sen(3t+2)$ $y(t)=7e$-0,4t$cos(5t-3)$ - Letras gregas nos gráficos: Letra Representação $\alpha$ \alpha $\beta$ \beta $\gamma$ \gamma $\delta$ \delta $\epsilon$ \epsilon $\kappa$ \kappa $\lambda$ \lambda $\mu$ \mu $\nu$ \nu $\omega$ \omega $\phi$ \phi $\pi$ \pi $\chi$ \chi $\psi$ \psi $\rho$ \rho $\sigma$ \sigma $\tau$ \tau $\upsilon$ \upsilon $\Sigma$ \Sigma $\Pi$ \Pi $\Lambda$ \Lambda $\Omega$ \Omega $\Gamma$ \Gamma - Funções stem, stairs e bar; Exercício: Plote em uma figura as funções $sen(x)$, usando stem; $cos(x)$, usando stairs e em uma segunda figura $tg(x)$, usando bar. Use um vetor $0\leq x\leq 2\pi$ com no máximo 100 posições.

Aula 13

22/Set

- Função polar; Exercício: Plote a função polar: $rho=sen(2\theta )*cos(2\theta )$ de $0\leq \theta \leq 2\pi$. - Mudar a espessura da linha com linewidth; - Mudar o tamanho da fonte com fontsize; - Mudar os eixos com gca; - Mudar a localização com location, orientação com orientation e tamanho da fonte com fontsize no quadro da legenda; - Ver a trajetória da função comet; - Barras de erro de aproximação com errorbar; Exercício (livro - adaptado - 10 p.253): Muitas aplicações utilizam a seguinte aproximação de "ângulo pequeno" para o seno com a finalidade de se obter um modelo mais simples que seja fácil de ser entendido e analisado. A aproximação estabelece que sen(x) $\simeq x$, em que x deve ser em radianos. Investigue a precisão desta aproximação com dois plotes. No primeiro, plote sen(x) versus x para $0\leq x\leq 1$. No segundo, plote o erro da aproximação (sen(x) - x) versus x para $0\leq x\leq 1$. - Plot em 3 dimensões com plot3; Exercício (livro - 28 p. 258): As equações paramétricas para uma hélice circular são: $x=a*cos(t)$ $y=a*sen(t)$ $z=b*t$ em que $a$ é o raio do caminho helicoidal e $b$ é uma constante que determina a "estreiteza" do caminho. Além disso, se $b>0$, a hélice tem a forma de um parafuso destro; se $b<0$, a hélice tem a forma de um parafuso canhoto. Obtenha uma plotagem tridimensional da hélice para os três casos a seguir e compare-os. Utilize $0\leq t\leq 10\pi$ e $a=1$. a) $b=0,1$; b) $b=0,2$; c) $b=-0,1$. - Criar uma malha 3D com meshgrid; - Plot de função de f(x,y) com mesh; - Rótulo no eixo z: zlabel; - Curva de níveis com contour, com a possibilidade de escolha do número de curvas; - Possibilidade de aparecer ou não os valores das curvas com o comando showtext seguido de on; - Comando para aparecer a malha 3D em apenas um sentido com waterfall; - Comando para fazer malha 3D com sombreamento: surf; - Comando para fazer malha 3D com sombreamento e curvas de níveis na projeção: surfc; - Comando para fazer malha 3D e curvas de níveis na projeção: meshc; - Comando para fazer malha 3D se alongar em z nas extremidades: meshz;

Aula 14

27/Set

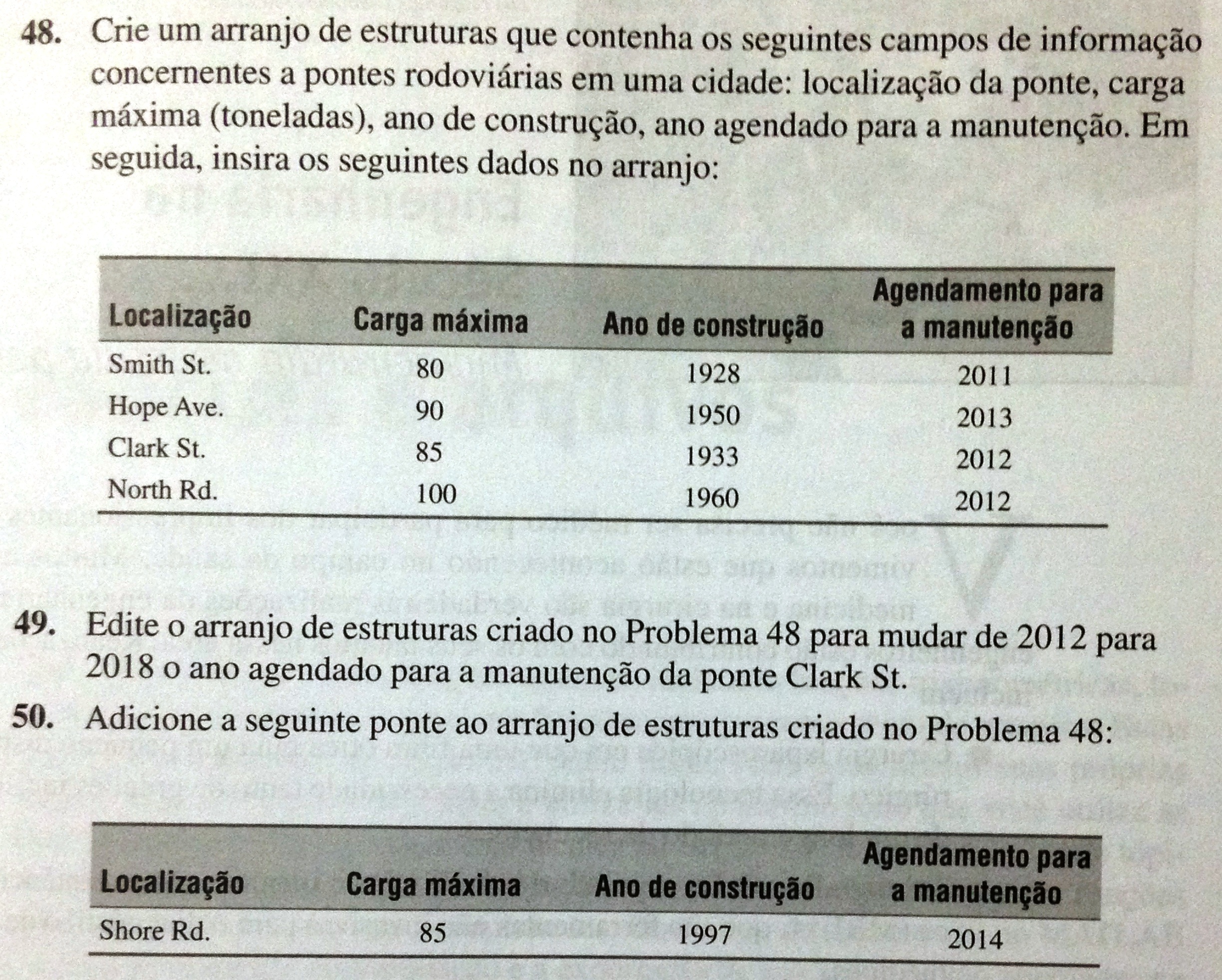
Exercício (livro - 30 p. 259): Obtenha as plotagens de superfície e de contorno para a função $z=x$2$-2xy+4y$2, mostrando o mínimo em $x=y=0$. - Comando polyfit, que ajusta o polinômio de grau n aos dados descritos por x e y; - Comando polyval, calcula a solução do polinômio a partir da escolha de um ponto; Exercício (livro - adaptado - Exemplo 6.2-1 p. 277): Os dados da tabela a seguir correspondem ao número de veículos (em milhões) que cruzam uma ponte a cada ano durante 10 anos. Ajuste um polinômio aos dados até a ordem 4, calcule o coeficiente de ajuste. Plote a "melhor" curva. Ano 1 2 3 4 5 6 7 8 9 10 Fluxo de veículos (milhões) 2,1 3,4 4,5 5,3 6,2 6,6 6,8 7 7,4 7,8 - Comando flip, representa o vetor de trás pra frente;

Aula 15

29/Set

Exercício (livro - adaptado - exemplo 6.2-2 p. 278): A tabela a seguir fornece dados de crescimento de uma determinada população de bactérias com o tempo. Ajuste uma equação para esses dados, calcule o coeficiente de ajuste e estime o fluxo no tempo 18 min. Plote a curva escolhida. Tempo (min) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Bactérias (ppm) 6 13 23 33 54 83 118 156 210 282 350 440 557 685 815 990 - Plotar dados da tabela, menu Tools e depois Basic Fitting, para escolher a melhor função que interpola os dados. - Comando rank saber a singularidade da matriz; - Função pseudoinversa (pinv) para resolver um sistema cuja solução garante a menor norma. Exercício (livro - 11 p. 363): Resolva as seguintes equações: ${\begin{alignedat}{7}7x&\;+&\;9y&\;-&\;9z&\;=&\;22\\3x&\;+&\;2y&\;-&\;4z&\;=&\;12\\x&\;+&\;5y&\;-&\;z&\;=&\;-2\\\end{alignedat}}$

Aula 16

04/Out

- Definição de Matriz Aumentada; - Comando rref para escalonar matriz; Exercício (livro - adaptado - T8.3-1 p. 343): Encontre duas soluções e o escalonamento para o seguinte conjunto: ${\begin{alignedat}{7}x&\;+&\;3y&\;+&\;2z&\;=&\;2\\x&\;+&\;y&\;+&\;z&\;=&\;4\\\end{alignedat}}$ Exercício (livro - adaptado - 12 p. 363): A tabela a seguir mostra quantas horas de processo são necessárias para que os reatores A e B produzam uma tonelada de cada um dos produtos químicos 1, 2 e 3. Os dois reatores são disponíveis por 35 e 40 horas por semana, respectivamente. Horas Produto 1 Produto 2 Produto 3 Reator A 6 2 10 Reator B 3 5 2 Sejam x, y e z o número de toneladas de cada um dos produtos 1, 2 e 3 que podem ser produzidos em uma semana. a) Utilize os dados na tabela para escrever duas equações em termos de x, y e z. Determine se existe um única solução. Encontre as relações entre x, y e z. b) Note que os valores negativos de x, y e z não têm significado nesse caso. Encontre as faixas de valores possíveis para x, y e z. c) Suponha que os lucros sejam de $200, $300 e $100 para cada produto 1, 2 e 3, respectivamente. Encontre os valores de x, y e z que maximizam os lucros. d) Suponha que os lucros sejam de $200, $500 e $100 para cada produto 1, 2 e 3, respectivamente. Encontre os valores de x, y e z que maximizam os lucros.

Aula 17

06/Out

Exercício (livro - adaptado - 13 p.364): Veja a figura abaixo. Suponha que os veículos não param dentro da rede. Um engenheiro de tráfego deseja saber se os fluxos de tráfego $f_{1},f_{2},...,f_{7}$ (em veículos por hora) podem ser calculados a partir dos fluxos medidos mostrados na figura. Se não, então determine quantos sensores de tráfego a mais precisam ser instalados e obtenha as expressões para os outros fluxos de tráfego em termos das quantidades medidas. 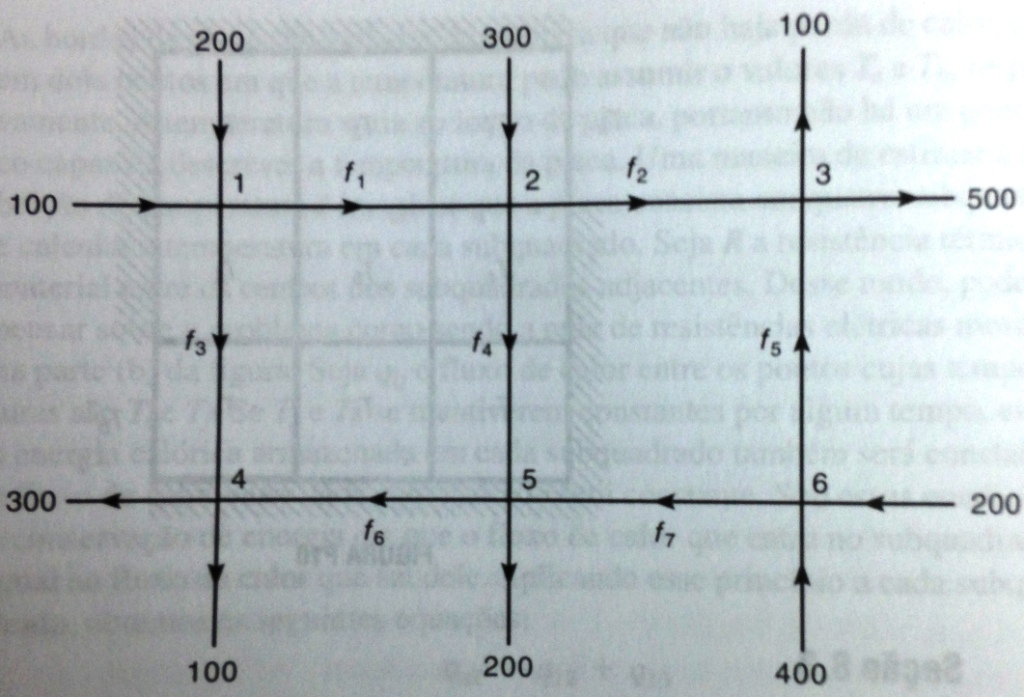- Caracteres especiais: Símbolo Descrição \b Backspace \n Mudança de linha \r Return \t Tabulação horizontal \\ Escreve o caracter \ \ Escreve o caracter ' %% Escreve o caracter % - Descritores de formato: Símbolo Descrição %c Um único caracter %d Número inteiro %e ou %E Número real escrito em notação científica %f Número real com parte decimal %g Notação mais compacta de %e e %f %o Número octal sem sinal %s String de caracteres %u Número inteiro sem sinal %x ou %X Hexadecimal (com letras minúsculas ou maiúsculas) Exercício: Fazer uma tabela com 3 colunas no Matlab que salve em um arquivo de texto externo, com o ângulo, seno e cosseno. Sendo o ângulo de $0$ a $2\pi$. - Comando msgbox para criar caixa de mensagem e opções extras como título, ícone pré-definido ou criado;

Aula 18

11/Out

- Caixa de diálogo de mensagem de aviso (warndlg); - Caixa de diálogo de mensagem de erro (errordlg); - Caixa de diálogo de mensagem de interrogação com múltipla escolha (questdlg); Exercício: Criar uma caixa de interrogação com múltipla escolha com as opções: Candidato A, Candidato B e Branco. Após apresente a escolha. - Caixa de diálogo de mensagem de ajuda (helpdlg); - Caixa de diálogo de introdução de dados (inputdlg); Exercício: Criar um código Matlab para abrir uma janela com a mensagem "O que você deseja comprar?" com múltiplas escolhas: Arroz, Feijão e Macarrão, quando escolher deve aparecer uma janela com opção para completar com a quantidade. De acordo com a quantidade calcular o preço total considerando o preço unitário do Arroz $6, do Feijão $10 e do Macarrão $5,50. Após a escolha deve aparecer uma terceira janela com opção de "sim" ou "não" para repetir o procedimento. Caso aceite repetir o código deve-se atualizar o cálculo com a nova escolha do produto e da quantidade.

Aula 19

13/Out
- Caixa de diálogo com lista de seleção de múltipla escolha (listdlg); Exercício: Criar um código com uma pergunta sobre preferência de filmes de acordo com o gênero, com múltiplas escolhas. Apresentar as opções escolhidas. - Caixa de diálogo com lista de seleção de escolha única também usando listdlg; - Exemplo 1 do uso de Graphical User Interface (GUI);

Aula 20

18/Out
- Término do Exemplo 1 do uso de Graphical User Interface (GUI); - Exemplo 2 do uso de Graphical User Interface (GUI);