Curso Matlab aplicado ao processamento de imagens - Aula 3
O processamento de imagens no Matlab é bastante facilitado. Nesta parte do curso, vamos estudar o básico do processamento de imagens, inicialmente para uma imagem em escala de cinza e depois para uma imagem colorida.
Inicialmente, salve as duas imagens abaixo no diretório de trabalho, e altere o diretório do Matlab para esta pasta. Para facilitar o trabalho, salve as variáveis como imagem1.jpeg e imagem2.jpeg.
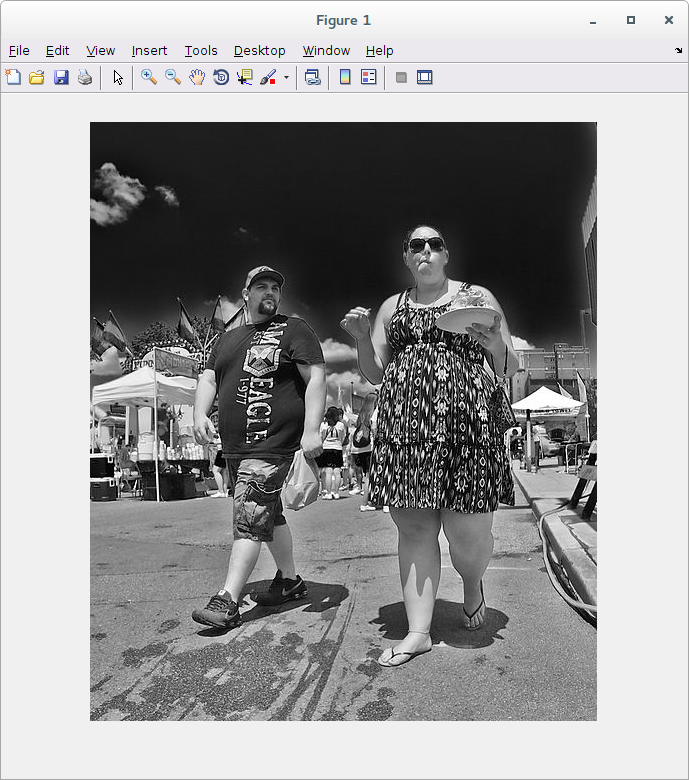
- imagem1.jpeg - Imagem de Daniel Teoli Jr, acessível em Link
- imagem2.jpeg - Imagem de Joao Carlos Medau, acessível em Link
Imagem em escala de cinza
Para ler uma imagem do computador, é utilizada a função imread:
>> x = imread('imagem1.jpeg');
Para visualizar a imagem, é utilizada a função imshow. Uma figura pode antes ser aberta, para evitar que a imagem seja exibida em cima de uma outra figura:
>> figure >> imshow(x)
Pelo comando whos, é possível perceber alguns atributos da imagem:
>> whos x Name Size Bytes Class Attributes x 599x507 303693 uint8
A imagem é para o Matlab uma matriz de 599x507, do tipo uint8. Sendo o valor um inteiro de 8 bits sem sinal, os valores podem ir de 0 a 255. No Matlab, valores mais próximos de 0 são de cor escura e valores mais próximos de 1 são de cor clara.
Negativo da imagem
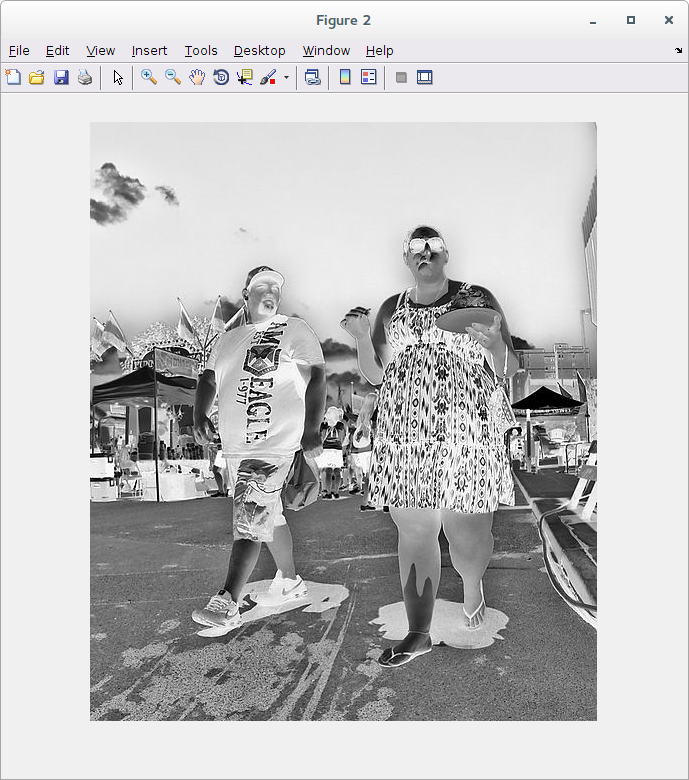
Para tirar o negativo da imagem, precisamos transformar valores próximos de 0 em valores próximos de 255, e vice-versa. Uma forma de fazer isso é subtrair 255 da imagem, e depois multiplicar por -1. Neste caso, porém, precisaremos realizar uma mudança no tipo do dado, pois a variável é inteira e sem sinal:
>> y = uint8(-1*(double(x)-255)); >> figure >> imshow(y)
Aumentando e reduzindo o brilho
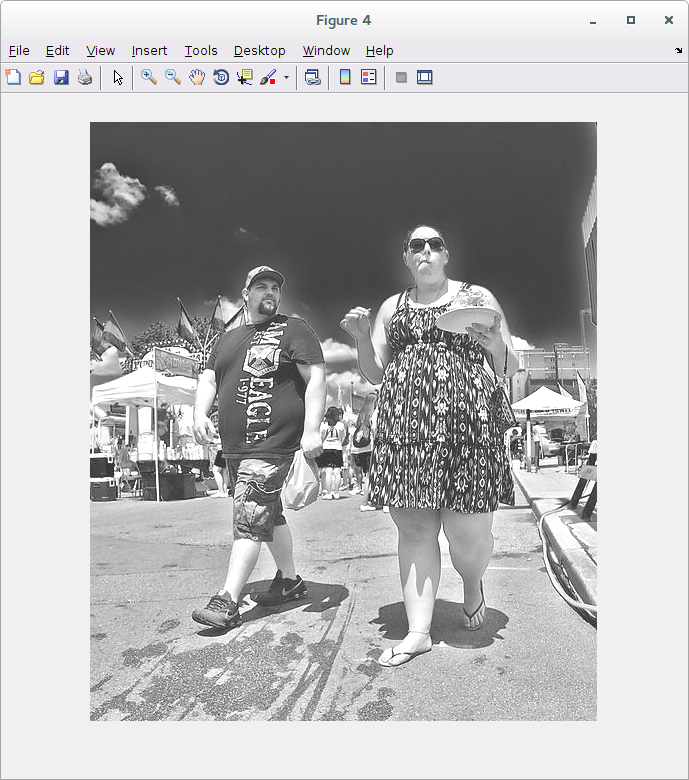
Aumentar o brilho significa deixar a imagem mais clara. Esta operação é feita somando uma constante à imagem:
>> z = x + 50; >> figure >> imshow(z)
Aumentando e reduzindo o contraste
Para aumentar o contraste, deixamos as cores claras mais claras e as cores escuras mais escuras. Isso pode ser feito facilmente no Matlab com algumas operações matemáticas. Primeiro, definimos o que são cores claras e o que são cores escuras, através de um limiar:
>> limiar = 180;
Esta variável indica que todos os valores com intensidade acima de 180 serão realçados enquanto todos abaixo de 180 serão atenuados. Com o limiar definido, fazemos uma operação de divisão:
>> a = double(x)/limiar;
O resultado da divisão será:
- Números entre 0 e 1, para valores de x menores que 180
- Números maiores que 1, para valores maiores que 180
Por isso a conversão de x para o tipo double foi necessária, já que o tipo uint8 não permite representar esses resultados. Após a divisão, o aumento no contraste é realizado por uma potenciação:
>> b = a.^2;
Essa operação faz com que os valores maiores que 1 fiquem ainda maiores, e os valores menores que 1 ainda menores. A operação é concluída ao multiplicar os valores pelo limiar, e converter os dados para uint8 novamente:
>> c = uint8(b*limiar);
Para observar o resultado, mostramos uma imagem ao lado da outra:
>> figure
>> subplot(1,2,1); imshow(x); title('Imagem original')
>> subplot(1,2,2); imshow(c); title('Imagem com o contraste aumentado')
O contraste pode ser ainda mais realçado ao utilizar potências maiores do que 2. Da mesma forma, podemos reduzir o contraste ao utilizar operações de raiz.
Binarização
A binarização é uma forma de separar regiões de imagens. A imagem resultante será branca nas regiões onde a intensidade da imagem original é maior que um determinado limiar e preta nas outras regiões. Essa operação é realizada de forma muito simples no Matlab. Para demonstrar isso, vamos usar o mesmo limiar utilizado no aumento de contraste. A binarização é realizada a partir de um teste:
>> d = x >= limiar;
Na linha acima, primeiro testamos se x é maior ou igual ao limiar. O Matlab retorna o lógico 1 quando o teste é verdadeiro e o lógico 0 quando o teste é falso. Esses resultados são armazenados na variável d.
Ao analisar o resultado (o imshow entende quando seu argumento é uma matriz binária), vemos que as partes mais claras da imagem ficaram brancas, enquanto as mais escuras ficaram pretas.
Adicionando uma marca d'água
Marcas d'água são pequenos logos incluídos nas imagens, normalmente utilizados para informação de autoria. Vamos adicionar o logo do IFSC na imagem em escala de cinza x que estamos utilizando até agora.
Primeiro, baixamos o logo do IFSC e salvamos na mesma pasta que estamos trabalhando, com o nome logo.gif. Lemos o arquivo no Matlab com:
>> marca = imread('logo.gif');
Para adicionar o logo como marca d'água, vamos transformar seus valores de forma que os seus valores máximos (cores brancas) fiquem com um valor 1. Para isso, executamos:
>> marca = double(marca)/double(max(max(marca)));
Assim, o valor máximo da imagem será dividido por ele mesmo, o que resultará em 1. Os outros valores ficarão entre 0 e 1.
Para poder multiplicar o logo pela imagem, precisamos corrigir a diferença no tamanho entre as matrizes. Para isso, vamos criar uma nova matriz, de nome camada, do mesmo tamanho da imagem. A matriz será composta de 1.
>> camada = ones(size(x));
Após isso, localizamos o logo dentro da camada, via indexação:
>> camada(1:size(marca,1), 1:size(marca,2)) = marca;
Assim, estamos dizendo que o logo ficará distribuído na matriz camada a partir da linha e coluna 1:
Após isso, basta realizar a multiplicação ponto a ponto das imagens, não esquecendo as conversões necessárias:
>> e = uint8(double(x) .* camada);
Como resultado, temos a imagem original com a marca do IFSC incluída na parte superior esquerda:
Suavização
Suavizar uma imagem significa reduzir sua nitidez. É realizado através do cálculo da média local ao redor de todos os pixels da imagem. No Matlab, isso é feito com a criação de uma matriz de média, chamada de máscara para realização de uma operação de convolução.
- Primeiro, uma matriz de média é criada. Ela deve ser quadrada, de tamanho ímpar, e a soma de seus elementos deve resultar em 1:
>> mask1 = (1/9)*[1 1 1; 1 1 1; 1 1 1]
mask1 =
0.1111 0.1111 0.1111
0.1111 0.1111 0.1111
0.1111 0.1111 0.1111
>> sum(sum(mask1))
ans =
1
- O cálculo da média é efetivado com o uso da função conv2. Essa função percorre a máscara por todos os pixels da imagem, realizando operações de multiplicação e soma.
>> suav1 = conv2(x,mask1);
- A imagem resultante tem porém, 1 pixel a mais em cada borda:
>> whos x suav1 Name Size Bytes Class Attributes suav1 601x509 2447272 double x 599x507 303693 uint8
- Assim, descartamos esses pixels:
>> suav1 = suav1(2:end-1, 2:end-1); >> size(suav1) ans = 599 507
- Para ver os resultados, exibimos as imagens lado a lado:
>> figure >> subplot(1,2,1); imshow(x) >> subplot(1,2,2); imshow(uint8(suav1))
Outros tipos de operadores de média podem ser utilizados, com máscaras maiores, ou mesmo não uniformes. Para máscaras uniformes, a função ones pode ser utilizada:
>> mask2 = (1/25)*ones(5,5)
mask2 =
0.0400 0.0400 0.0400 0.0400 0.0400
0.0400 0.0400 0.0400 0.0400 0.0400
0.0400 0.0400 0.0400 0.0400 0.0400
0.0400 0.0400 0.0400 0.0400 0.0400
0.0400 0.0400 0.0400 0.0400 0.0400
>> mask3 = (1/15)*[1 2 1; 2 3 2; 1 2 1]
mask3 =
0.0667 0.1333 0.0667
0.1333 0.2000 0.1333
0.0667 0.1333 0.0667
Detecção de bordas
A detecção de bordas em imagens é feita de forma semelhante à suavização, porém uma máscara diferente é utilizada. Neste curso vamos usar uma máscara específica, de Sobel, mas existem muitas outras que podem ser utilizadas, com vantagens e desvantagens específicas. A máscara de Sobel é definida para bordas verticais e horizontais, respectivamente:
>> sobel_v = [-1, -2, -1; 0, 0, 0; 1, 2, 1]
sobel_v =
-1 -2 -1
0 0 0
1 2 1
>> sobel_h = [-1, 0, 1; -2, 0, 2; -1, 0, 1]
sobel_h =
-1 0 1
-2 0 2
-1 0 1
Ao aplicar os operadores na imagem, usando a função conv2, temos como resultado as imagens abaixo:
>> borda_v = conv2(x,sobel_v);
>> borda_h = conv2(x,sobel_h);
>> borda_v = borda_v(2:end-1,2:end-1);
>> borda_h = borda_h(2:end-1,2:end-1);
>> figure
>> subplot(1,2,1); imshow(uint8(borda_v)); title('Bordas verticais da imagem')
>> subplot(1,2,2); imshow(uint8(borda_h)); title('Bordas horizontais da imagem')
Pode também ser feita a soma das componentes verticais e horizontais das bordas:
>> borda = borda_v + borda_h;
>> figure
>> subplot(1,2,1); imshow(x); title('Imagem original')
>> subplot(1,2,2); imshow(uint8(borda)); title('Bordas da imagem')
Imagem colorida
Agora vamos ler a imagem colorida, e verificar as diferenças com relação à escala de cinza:
>> a = imread('imagem2.jpeg');
>> figure
>> imshow(a)
Ao executar o comando whos, percebemos as diferenças entre as imagens:
>> whos a Name Size Bytes Class Attributes a 388x640x3 744960 uint8
Repare que, da mesma forma que a imagem em escala de cinza, a imagem colorida é composta por valores do tipo uint8. Porém, neste caso, há uma terceira dimensão disponível. É a partir desta nova dimensão que as características de cor são passadas. Uma imagem colorida é composta por 3 planos de cor, cada um representando a quantidade disponível das cores vermelho, verde ou azul. Quanto maior o valor de um elemento do plano, maior a quantidade da cor correspondente. Com isso, temos as componentes RGB da imagem.
Criando uma imagem da paleta de cores
Vamos criar uma imagem que indica a quantidade de cada cor disponível. Para isso, vamos separar uma figura do Matlab em 4 sub-figuras com a função subplot. Primeiro, abrimos uma nova figura, e na primeira subfigura, exibimos a imagem colorida:
>> figure
>> subplot(2,2,1); imshow(a); title('Imagem colorida')
Na segunda sub-figura, plotamos as componentes de vermelho:
>> subplot(2,2,2); imshow(a(:,:,1)); title('Componentes de vermelho - R')
Na terceira, os componentes de verde:
>> subplot(2,2,3); imshow(a(:,:,2)); title('Componentes de verde - G')
Na quarta, os componentes de azul:
>> subplot(2,2,4); imshow(a(:,:,3)); title('Componentes de azul - B')
Repare nas diferenças entre as 3 figuras de cor:
Paleta de cores modificada
Visando deixar a imagem da paleta de cores um pouco mais visual, vamos criar imagens baseadas na imagem inicial. Criamos 3 matrizes, b_R, b_G, e b_B, do tamanho da imagem inicial, inicialmente com zeros. Não esquecer que o tipo dos dados deve ser uint8.
>> b_R = uint8(zeros(size(a))); >> b_G = uint8(zeros(size(a))); >> b_B = uint8(zeros(size(a)));
Após isso, atribuímos o primeiro plano da imagem original ao primeiro plano da imagem b_R. O segundo plano da imagem original é atribuído ao segundo plano da imagem b_G, e o terceiro plano ao terceiro plano da imagem b_B:
>> b_R(:,:,1) = a(:,:,1); >> b_G(:,:,2) = a(:,:,2); >> b_B(:,:,3) = a(:,:,3);
Feito isso, realizamos os subplots da mesma forma como antes:
>> figure
>> subplot(2,2,1); imshow(a); title('Imagem colorida')
>> subplot(2,2,2); imshow(b_R); title('Componentes de vermelho - R')
>> subplot(2,2,3); imshow(b_G); title('Componentes de verde - G')
>> subplot(2,2,4); imshow(b_B); title('Componentes de azul - B')
Com essa nova imagem, deixamos ainda mais claro como estão distribuídas as componentes de cor.
Projeto final
O projeto consiste na criacao de uma ferramenta de processamento de imagens. O usuario ira entrar com o nome do arquivo num campo de texto, e clicar num botao para a realizacao da leitura da imagem. A imagem sera lida pelo sistema e exibida no eixo da imagem original. Na segunda area da interface, varias operacoes poderao ser selecionadas, e os resultados serao exibidos no eixo da imagem processada.