|
|
| Linha 136: |
Linha 136: |
| | |<math>Z_{in(z)}= Z_o {Z_L + Z_o tanh \gamma z \over Z_o + Z_L tanh \gamma z}</math> | | |<math>Z_{in(z)}= Z_o {Z_L + Z_o tanh \gamma z \over Z_o + Z_L tanh \gamma z}</math> |
| | |} | | |} |
| | + | |
| | + | |
| | + | == Potência transmitida, recebida e de retorno == |
Edição das 20h14min de 8 de setembro de 2015
Uma linha de transmissão possui uma impedância característica Zo definida pela relação entre a  e
e  . Considere que uma carga
. Considere que uma carga  é acoplada a um dos terminais da linha (figura 1)
é acoplada a um dos terminais da linha (figura 1)
figura 1: Linha com carga
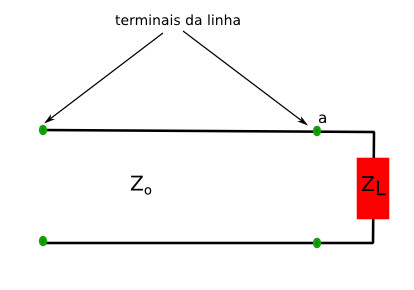
Sobre essa carga teremos uma tensão  , fazendo circular uma corrente
, fazendo circular uma corrente  .
.
Na linha teremos as tensões  e
e  e as correntes
e as correntes  e
e  , conforme indicado no figura 2.
, conforme indicado no figura 2.
figura 2: Linhas com carga com tensões e correntes.
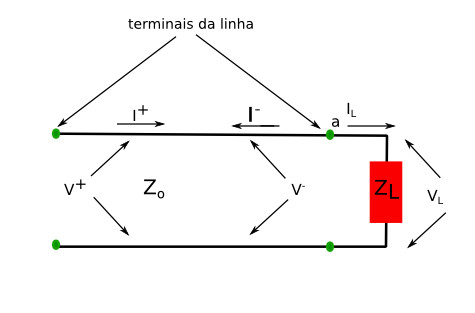
podemos escrever  como:
como:

Mas no nó terminal a da linha a tensão é a soma fasorial de  e
e  , portanto
, portanto

do nó a podemos retirar ainda a relação:

considerando o nó a como o ponto onde z = 0:

como

podemos escrever:

fazendo algumas manipulações algébricas:

À relação  chamamos de coeficiente de reflexão e representamos pela letra grega Γ
chamamos de coeficiente de reflexão e representamos pela letra grega Γ
Para diferenciar de outro ponto da linha iremos identificar o coeficiente de reflexão na carga por 

|
coeficiente de reflexão afastado da carga
O valor de Γ em qualquer ponto da linha será dado pela relação entre  , sendo assim para um ponto afastado uma distância l da carga teremos:
, sendo assim para um ponto afastado uma distância l da carga teremos:


|
Impedância de entrada
A relação entre a tensão e a corrente total em um determinado ponto da linha de transmissão é conhecida como Zin, impedância de entrada.
figura 3: Impedância de entrada - é a impedância vista em um ponto da linha.
Observe que não estamos nos referindo a Zo (impedância característica) esta corresponde a relação  , enquanto que Zin é dada por:
, enquanto que Zin é dada por:

substituindo  e
e  por:
por:


temos:

agora substituindo  :
:




dividindo numerador e denominador por  e lembrando que:
e lembrando que:

temos:

|
Potência transmitida, recebida e de retorno




































