Mudanças entre as edições de "CAL3-EngTel (Plano de Ensino)"
Ir para navegação
Ir para pesquisar
| Linha 13: | Linha 13: | ||
;Objetivos | ;Objetivos | ||
| + | ; Que o estudante seja capaz de: | ||
| + | ;- Compreender a relação entre a representação paramétrica de curvas e as funções vetoriais; | ||
| + | ;- Compreender o cálculo de integrais múltiplas de funções de várias variáveis e sua interpretação geométrica como volume do sólido. | ||
| + | ;- Calcular grandezas físicas representadas por meio de campos vetoriais e interpretar o significado de seua gradientes e rotacionais. | ||
| + | ;- Conhecer a definição, as principais propriedades e métodos de resolução de integrais de linha e de superfície de campos vetoriais. | ||
;Ementa | ;Ementa | ||
| − | :Funções vetoriais de uma variável. Parametrização, representação geométrica e propriedades de curvas. Funções vetoriais de várias variáveis. Derivadas direcionais e campos gradientes. Definições e aplicações das integrais curvilíneas. Estudo das superfícies, cálculo de áreas, definições e aplicações físicas das integrais de superfície. | + | :Funções vetoriais de uma variável. Parametrização, representação geométrica e propriedades de curvas. Integrais múltipla: integrais duplas e triplas, cálculo de volumes e integrais em coordenadas parametrizadas de funções de várias variáveis. Funções vetoriais de várias variáveis. Derivadas direcionais e campos gradientes. Aplicações em eletromagnetismo. Definições e aplicações das integrais curvilíneas. Estudo das superfícies, cálculo de áreas, definições e aplicações físicas das integrais de superfície. |
;Conteúdo Programático | ;Conteúdo Programático | ||
| − | :1.Funções vetoriais de uma variável. Parametrização, representação geométrica e propriedades de curvas (16h). <br>2.Funções vetoriais de várias variáveis (16h). <br> | + | :1.Funções vetoriais de uma variável. Parametrização, representação geométrica e propriedades de curvas (16h). <br> 2. Integrais múltiplas e aplicações. (14h) <br> 3.Funções vetoriais de várias variáveis (16h). <br>4.Derivadas direcionais e campos gradientes. Definições e aplicações das integrais curvilíneas (10h). <br>5.Estudo das superfícies, cálculo de áreas, definições e aplicações físicas das integrais de superfície (10h). <br>Avaliações (6h). |
;Cronograma de atividades | ;Cronograma de atividades | ||
| − | + | {{Cronograma-top}} | |
| + | {{Cl|1 |27/3 | 2 | Apresentação do Plano de ensino. Introdução às funções vetoriais descritas por equações paramétricas. | Quadro e giz.}} | ||
| + | {{Cl|2 |1/4 | 2 | Estudo das equações paramétricas e coordenadas polares. | Quadro e giz.}} | ||
| + | {{Cl|3 |3/4 | 2 | Cálculo das tangentes à curvas descritas por meio de coordenadas polares e paramétricas. | Quadro e giz. Folha fotocopiada.}} | ||
| + | {{Cl|4 |8/4 | 2 | Cálculo de comprimento de arco e área de superfície em coordenadas polares e paramétricas. | Quadro e giz.}} | ||
| + | {{Cl|5 |10/4 | 2 | Introdução às coordenadas cilíndricas e esféricas. Definição, compreensão. | Quadro e giz.}} | ||
| + | {{Cl|6 |15/4 | 2 | Propriedades de curvas descritas por meio de coordenadas esféricas e cilíndricas. Conversão para coordenadas cartesianas. Vizualização por meio se software de plotagem. | Quadro e giz. Projeção de simulação com software de plotagem de funções.}} | ||
| + | {{Cl|7 |17/4 | 2 | Operações com funções vetoriais no plano e nos espaço. Cálculo de limites, derivadas e integrais. | Quadro e giz. Folha fotocopiada.}} | ||
| + | {{Cl|8 |22/4 | 2 | Outras operações: derivação do produto vetorial. Cálculo de comprimento de arco de curvas paramétricas, versor tangente, normal e binormal. Curvatura. | Quadro e giz.}} | ||
| + | {{Cl|9 |24/4 | 2 | Aplicações de funções vetoriais. | Quadro e giz. Folha fotocopiada.}} | ||
| + | {{Cl|10 |29/4 | 2 | Exercícios. | Quadro e giz.}} | ||
| + | {{Cl|11 |6/5 | 2 | Preparação para a avaliação. | Quadro e giz.}} | ||
| + | {{Cl|12 |8/5 | 2 | Avaliação individual e por escrito. Conteúdos: Funções vetoriais de uma variável e coordenadas polares, cilíndricas e esféricas. | Quadro e giz. Folha fotocopiada.}} | ||
| + | {{Cl|13 |13/5 | 2 | Introdução às integrais múltiplas. Integrais duplas sobre retângulo e volume de sólido. | Quadro e giz.}} | ||
| + | {{Cl|14 |15/5 | 2 | Propriedades de integral dupla e métodos de cálculo. | Quadro e giz.}} | ||
| + | {{Cl|15 |20/5 | 2 | Mudança de variável em integral dupla e integral dupla em coordenadas polares. | Quadro e giz.}} | ||
| + | {{Cl|16 |22/5 | 2 | Aplicações de integral dupla (em cálculo de volumes e na física). | Quadro e giz.}} | ||
| + | {{Cl|17 |27/5 | 2 | Exercícios. | Quadro e giz. Folha fotocopiada.}} | ||
| + | {{Cl|18 |29/5 | 2 | Integrais triplas sobre cubo e volume. | }} | ||
| + | {{Cl|19 |3/6 | 2 | Propriedades de integral tripla e métodos de cálculo. | Quadro e giz.}} | ||
| + | {{Cl|20 |5/6 | 2 | Mudança de variável em integral tripla. | Quadro e giz.}} | ||
| + | {{Cl|21 |10/6 | 2 | Integral tripla em coordenadas esféricas e cilíndricas. | Quadro e giz.}} | ||
| + | {{Cl|22 |12/6 | 2 | Aplicações de integral tripla na física. | Quadro e giz. Software de plotagem. Folha fotocopiada.}} | ||
| + | {{Cl|23 |17/6 | 2 | Exercícios. | }} | ||
| + | {{Cl|24 |19/6 | 2 | Avaliação Individual e por escrito de integrais múltiplas. | Folha fotocopiada.}} | ||
| + | {{Cl|25 |24/6 | 2 | Introdução a campos escalares e vetoriais. Representação geométrica. | Quadro e giz.}} | ||
| + | {{Cl|26 |26/6 | 2 | Derivada Direcional e Gradiente de campo escalar. Aplicações de gradiente. | Quadro e giz.}} | ||
| + | {{Cl|27 |1/7 | 2 | Divergência e Rotacional de campo vetorial. Aplicações em eletromagnetismo.| Quadro e giz.}} | ||
| + | {{Cl|28 |3/7 | 2 | Integral de linha. Teorema fundamental das integrais de linha. | }} | ||
| + | {{Cl|29 |8/7 | 2 | Teorema de Green. Superfícies paramétricas e suas áreas. | Quadro e giz.}} | ||
| + | {{Cl|30 |10/7 | 2 | Integrais de superfícies. Teorema de Stokes. | Quadro e giz.}} | ||
| + | {{Cl|31 |15/7 | 2 | Teorema da divergência. | Quadro e giz.}} | ||
| + | {{Cl|32 |17/7 | 2 | Integrais de superfícies. Teorema de Stokes. | Quadro e giz.}} | ||
| + | {{Cl|33 |22/7 | 2 | Teorema da divergência. | Quadro e giz.}} | ||
| + | {{Cl|34 |24/7 | 2 | Avaliação Individual e por escrito de integrais múltiplas. | Folha fotocopiada.}} | ||
| + | {{Cl|35 |29/7 | 2 | Aula para recuperação. | Quadro e giz.}} | ||
| + | {{Cl|36 |31/7 | 2 | Avaliação de recuperação. | Folha fotocopiada.}} | ||
| + | |||
;Estratégias de ensino utilizadas | ;Estratégias de ensino utilizadas | ||
| + | * Aula expositiva e dialogada. Execução de exercícios para automatizar procedimentos de resolução e aprofundar a compreensão. Experimentação e simulações por meio de softwares de plotagem de gráficos de funções parametrizadas e em sistemas alternativos de coordenadas. Realização de trabalho relacionando os conhecimentos matemáticos trabalhados com as aplicações físicas, particularmente em eletromagnetismo. | ||
;Critérios e instrumentos de avaliação | ;Critérios e instrumentos de avaliação | ||
| + | |||
| + | Serão avaliadas a compreensão e a capacidade de resolução de problemas e de cálculo com os entes matemáticos apresentados, por meio de avaliações individuais e por escrito, além da entrega de trabalho sobre as aplicações dos conceitos trabalhados na área de física, a ser realizado em dupla. Para a aprovação será necessária a obtenção de no mínimo conceito C em cada uma das avaliações (incluindo o trabalho), com a possibilidade de realização de avaliação de recuperação sobre cada tópico em horário alternativo ao horário de aula (excluindo desse caso o trabalho). | ||
;Atividades Complementares | ;Atividades Complementares | ||
| + | Simulação e experimentação por meio de software | ||
;Bibliografia Básica | ;Bibliografia Básica | ||
:1.FLEMMING, Diva Maria; GONÇALVES, Mírian Buss. '''CÁLCULO B''': Funções de várias variáveis, integrais múltiplas, integrais curvilíneas e de superfície. São Paulo: Prentice Hall Brasil, 2007. 448 p. ISBN 978-8576051169. <br>2.STEWART, James. '''CÁLCULO 2''': Tradução da 6ª edição norte-americana. São Paulo: Cengale, 2009. 688 p. ISBN 978-8522106615. | :1.FLEMMING, Diva Maria; GONÇALVES, Mírian Buss. '''CÁLCULO B''': Funções de várias variáveis, integrais múltiplas, integrais curvilíneas e de superfície. São Paulo: Prentice Hall Brasil, 2007. 448 p. ISBN 978-8576051169. <br>2.STEWART, James. '''CÁLCULO 2''': Tradução da 6ª edição norte-americana. São Paulo: Cengale, 2009. 688 p. ISBN 978-8522106615. | ||
;Bibliografia Complementar | ;Bibliografia Complementar | ||
| − | :3. LEITHOLD, Louis. '''Cálculo com Geometria Analítica Vol.2'''. São Paulo: Harbra, 1994. ISBN 8529402065. | + | :3. LEITHOLD, Louis. '''Cálculo com Geometria Analítica Vol.2'''. São Paulo: Harbra, 1994. ISBN 8529402065.<br> 4. ANTON. Howard. BIVENS, Irl. DAVIS, Stephen.'''Cálculo - Volume II.''' São Paulo: Bookman, 2007. 672 p. ISBN 978-85-60031-80-1. |
;Professores Responsáveis | ;Professores Responsáveis | ||
Edição das 14h41min de 22 de abril de 2013

|
MINISTÉRIO DA EDUCAÇÃO |
Plano de Ensino de 2013-1
- Dados gerais
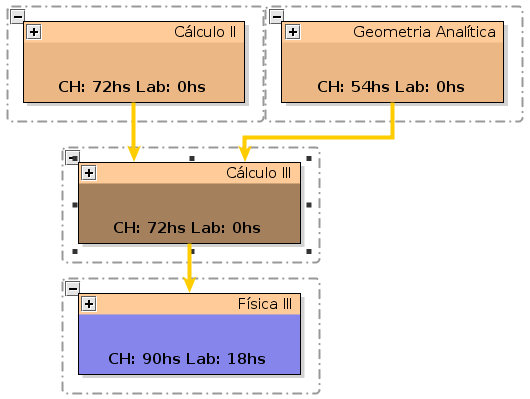
[[Arquivo:
|right | thumb |
250px | UCs vizinhas]]
- COMPONENTE CURRICULAR: CAL3 - CÁLCULO III
- CARGA HORÁRIA: 4 HORAS/SEMANA 72 HORAS. TEÓRICA = 72 HORAS. LABORATÓRIO = 0 HORAS
- PRÉ REQUISITOS: CAL2, GAL
- DISCIPLINAS SUCESSORAS: FSC3
- MÓDULO BÁSICO
- Objetivos
- Que o estudante seja capaz de
- - Compreender a relação entre a representação paramétrica de curvas e as funções vetoriais;
- - Compreender o cálculo de integrais múltiplas de funções de várias variáveis e sua interpretação geométrica como volume do sólido.
- - Calcular grandezas físicas representadas por meio de campos vetoriais e interpretar o significado de seua gradientes e rotacionais.
- - Conhecer a definição, as principais propriedades e métodos de resolução de integrais de linha e de superfície de campos vetoriais.
- Ementa
- Funções vetoriais de uma variável. Parametrização, representação geométrica e propriedades de curvas. Integrais múltipla: integrais duplas e triplas, cálculo de volumes e integrais em coordenadas parametrizadas de funções de várias variáveis. Funções vetoriais de várias variáveis. Derivadas direcionais e campos gradientes. Aplicações em eletromagnetismo. Definições e aplicações das integrais curvilíneas. Estudo das superfícies, cálculo de áreas, definições e aplicações físicas das integrais de superfície.
- Conteúdo Programático
- 1.Funções vetoriais de uma variável. Parametrização, representação geométrica e propriedades de curvas (16h).
2. Integrais múltiplas e aplicações. (14h)
3.Funções vetoriais de várias variáveis (16h).
4.Derivadas direcionais e campos gradientes. Definições e aplicações das integrais curvilíneas (10h).
5.Estudo das superfícies, cálculo de áreas, definições e aplicações físicas das integrais de superfície (10h).
Avaliações (6h).
- Cronograma de atividades
- Estratégias de ensino utilizadas
- Aula expositiva e dialogada. Execução de exercícios para automatizar procedimentos de resolução e aprofundar a compreensão. Experimentação e simulações por meio de softwares de plotagem de gráficos de funções parametrizadas e em sistemas alternativos de coordenadas. Realização de trabalho relacionando os conhecimentos matemáticos trabalhados com as aplicações físicas, particularmente em eletromagnetismo.
- Critérios e instrumentos de avaliação
- Atividades Complementares
- Bibliografia Básica
- 1.FLEMMING, Diva Maria; GONÇALVES, Mírian Buss. CÁLCULO B: Funções de várias variáveis, integrais múltiplas, integrais curvilíneas e de superfície. São Paulo: Prentice Hall Brasil, 2007. 448 p. ISBN 978-8576051169.
2.STEWART, James. CÁLCULO 2: Tradução da 6ª edição norte-americana. São Paulo: Cengale, 2009. 688 p. ISBN 978-8522106615.
- Bibliografia Complementar
- 3. LEITHOLD, Louis. Cálculo com Geometria Analítica Vol.2. São Paulo: Harbra, 1994. ISBN 8529402065.
4. ANTON. Howard. BIVENS, Irl. DAVIS, Stephen.Cálculo - Volume II. São Paulo: Bookman, 2007. 672 p. ISBN 978-85-60031-80-1.
- Professores Responsáveis
- Elenira Vilela
| Aula | Data | Horas | Conteúdo | Recursos |
|---|---|---|---|---|
| 1 | 27/3 | 2 | Apresentação do Plano de ensino. Introdução às funções vetoriais descritas por equações paramétricas. | Quadro e giz. |
| 2 | 1/4 | 2 | Estudo das equações paramétricas e coordenadas polares. | Quadro e giz. |
| 3 | 3/4 | 2 | Cálculo das tangentes à curvas descritas por meio de coordenadas polares e paramétricas. | Quadro e giz. Folha fotocopiada. |
| 4 | 8/4 | 2 | Cálculo de comprimento de arco e área de superfície em coordenadas polares e paramétricas. | Quadro e giz. |
| 5 | 10/4 | 2 | Introdução às coordenadas cilíndricas e esféricas. Definição, compreensão. | Quadro e giz. |
| 6 | 15/4 | 2 | Propriedades de curvas descritas por meio de coordenadas esféricas e cilíndricas. Conversão para coordenadas cartesianas. Vizualização por meio se software de plotagem. | Quadro e giz. Projeção de simulação com software de plotagem de funções. |
| 7 | 17/4 | 2 | Operações com funções vetoriais no plano e nos espaço. Cálculo de limites, derivadas e integrais. | Quadro e giz. Folha fotocopiada. |
| 8 | 22/4 | 2 | Outras operações: derivação do produto vetorial. Cálculo de comprimento de arco de curvas paramétricas, versor tangente, normal e binormal. Curvatura. | Quadro e giz. |
| 9 | 24/4 | 2 | Aplicações de funções vetoriais. | Quadro e giz. Folha fotocopiada. |
| 10 | 29/4 | 2 | Exercícios. | Quadro e giz. |
| 11 | 6/5 | 2 | Preparação para a avaliação. | Quadro e giz. |
| 12 | 8/5 | 2 | Avaliação individual e por escrito. Conteúdos: Funções vetoriais de uma variável e coordenadas polares, cilíndricas e esféricas. | Quadro e giz. Folha fotocopiada. |
| 13 | 13/5 | 2 | Introdução às integrais múltiplas. Integrais duplas sobre retângulo e volume de sólido. | Quadro e giz. |
| 14 | 15/5 | 2 | Propriedades de integral dupla e métodos de cálculo. | Quadro e giz. |
| 15 | 20/5 | 2 | Mudança de variável em integral dupla e integral dupla em coordenadas polares. | Quadro e giz. |
| 16 | 22/5 | 2 | Aplicações de integral dupla (em cálculo de volumes e na física). | Quadro e giz. |
| 17 | 27/5 | 2 | Exercícios. | Quadro e giz. Folha fotocopiada. |
| 18 | 29/5 | 2 | Integrais triplas sobre cubo e volume. | |
| 19 | 3/6 | 2 | Propriedades de integral tripla e métodos de cálculo. | Quadro e giz. |
| 20 | 5/6 | 2 | Mudança de variável em integral tripla. | Quadro e giz. |
| 21 | 10/6 | 2 | Integral tripla em coordenadas esféricas e cilíndricas. | Quadro e giz. |
| 22 | 12/6 | 2 | Aplicações de integral tripla na física. | Quadro e giz. Software de plotagem. Folha fotocopiada. |
| 23 | 17/6 | 2 | Exercícios. | |
| 24 | 19/6 | 2 | Avaliação Individual e por escrito de integrais múltiplas. | Folha fotocopiada. |
| 25 | 24/6 | 2 | Introdução a campos escalares e vetoriais. Representação geométrica. | Quadro e giz. |
| 26 | 26/6 | 2 | Derivada Direcional e Gradiente de campo escalar. Aplicações de gradiente. | Quadro e giz. |
| 27 | 1/7 | 2 | Divergência e Rotacional de campo vetorial. Aplicações em eletromagnetismo. | Quadro e giz. |
| 28 | 3/7 | 2 | Integral de linha. Teorema fundamental das integrais de linha. | |
| 29 | 8/7 | 2 | Teorema de Green. Superfícies paramétricas e suas áreas. | Quadro e giz. |
| 30 | 10/7 | 2 | Integrais de superfícies. Teorema de Stokes. | Quadro e giz. |
| 31 | 15/7 | 2 | Teorema da divergência. | Quadro e giz. |
| 32 | 17/7 | 2 | Integrais de superfícies. Teorema de Stokes. | Quadro e giz. |
| 33 | 22/7 | 2 | Teorema da divergência. | Quadro e giz. |
| 34 | 24/7 | 2 | Avaliação Individual e por escrito de integrais múltiplas. | Folha fotocopiada. |
| 35 | 29/7 | 2 | Aula para recuperação. | Quadro e giz. |
| 36 | 31/7 | 2 | Avaliação de recuperação. | Folha fotocopiada. |