Mudanças entre as edições de "CAL1-EngTel (Plano de Ensino)"
Ir para navegação
Ir para pesquisar
| Linha 50: | Linha 50: | ||
;Bibliografia Básica | ;Bibliografia Básica | ||
| − | + | # LEITHOLD, LOUIS '''O CÁLCULO COM GEOMETRIA ANALÍTICA Vol.1'''; 3ª ed. São Paulo:HABRA, 1994. 788p. ISBN 8529400941 | |
| − | + | # FLEMMING, DIVA. GONÇALVES, MIRIAN '''CÁLCULO A'''; 6ª ed. SÃO PAULO:Pearson, 2007. 464p. ISBN 9788576051152 | |
| + | # STEWART, JAMES '''CÁLCULO Vol.1'''; trad.7ª ed. SÃO PAULO:Cengage Learning, 2014. 664p. ISBN 9788522112586 | ||
;Bibliografia Complementar | ;Bibliografia Complementar | ||
| − | + | # GUIDORIZZI, HAMILTON '''CÁLCULO Vol.1'''; 5ª ed. [S.l]:LTC, 2001. 652p. ISBN 9788521612599 | |
| + | # SIMMONS, George '''Cálculo com geometria analítica: volume 1'''; 1ª ed. São Paulo:Pearson, 2010. 829p. ISBN 9780074504116 | ||
| + | # MEDEIROS, Valéria Zuma '''Pré-calculo'''; 2ª ed. São Paulo:Cengage Learning, 2010. 538p. ISBN 9788522107353 | ||
=ANEXOS= | =ANEXOS= | ||
Edição das 17h52min de 13 de março de 2014

|
MINISTÉRIO DA EDUCAÇÃO |
Plano de Ensino de 2012-1 - atual
- Dados gerais
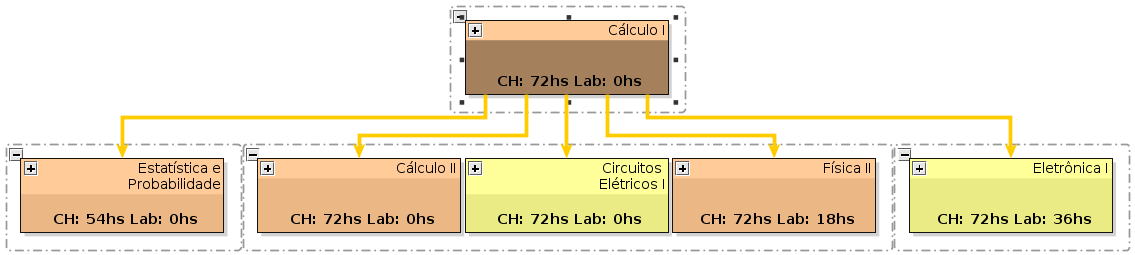
- COMPONENTE CURRICULAR: CAL1 - CÁLCULO I
- CARGA HORÁRIA: 4 HORAS/SEMANA 72 HORAS. TEÓRICA = 72 HORAS. LABORATÓRIO = 0 HORAS
- Objetivos
- Ao concluir o componente curricular o discente deverá ser capaz de:
- 1. Usar conhecimentos relacionados ao conjunto dos números reais e complexos e funções no cálculo de limites, derivadas e integrais.
- 2. Compreender o conceito de limites.
- 3. Calcular limites.
- 4. Compreender o conceito de derivada.
- 5. Calcular derivadas.
- 6. Compreender os conceitos da integral.
- 7. Calcular integrais.
- 8. Aplicar os conceitos de derivada e integral em problemas.
- Ementa
- Números reais. Números complexos. Funções reais de uma variável real. Limites e continuidade. Derivadas. Regras de derivação. Aplicações de derivadas. Integral indefinida. Regras de integração. Técnicas de integração. Integral definida. Teorema fundamental do cálculo. Aplicações de integrais definidas. Integrais impróprias.
- Conteúdo Programático
- 1. Números Reais e Números complexos (6h).
- 2. Funções: conceito e notação; conjunto e imagem; tipos de funções e seus gráficos (4h).
- 3. Limites: interpretação geométrica. Limites laterais. Limites infinitos. Limites em função contínua (8h).
- 4. Derivadas: interpretação geométrica. Derivada de uma função. Derivada de potências para expoentes racionais. Derivação de funções transcendentes. Regra da cadeia. Diferenciação implícita. Valores máximos e mínimos. Pontos de inflexão. Extremos relativos. Teste da derivada primeira (12h).
- 5. Aplicação das derivadas em problemas de otimização (4h).
- 6. Integração e suas aplicações: antiderivadas e integrais indefinidas. Regra geral da potência, integrais exponenciais e logarítmicas (4h).
- 7. Área e teorema fundamental do cálculo. Área de uma região delimitada por dois gráficos, integral definida como limite de uma soma, volumes de sólidos de revolução (4h).
- 8. Técnicas de integração: integração por substituição, integração por partes. Substituição trigonométrica (10h).
- 9. Frações parciais (8h).
- 10. Integrais impróprias (6h).
- Avaliações (6h).
- Estratégias de ensino utilizadas
- Aulas expositivas e dialogadas com o uso de lousa, giz, projetor multimídia, resolução de exercícios e utilização de softwares matemáticos.
- Critérios e instrumentos de avaliação
- A avaliação compreende os seguintes elementos:
- 1. Desempenho em sala de aula;
- 2. Participação nas atividades curriculares;
- 3. Provas escritas;
- 4. Trabalhos - Exercícios realizados extra-classe.
- Bibliografia Básica
- LEITHOLD, LOUIS O CÁLCULO COM GEOMETRIA ANALÍTICA Vol.1; 3ª ed. São Paulo:HABRA, 1994. 788p. ISBN 8529400941
- FLEMMING, DIVA. GONÇALVES, MIRIAN CÁLCULO A; 6ª ed. SÃO PAULO:Pearson, 2007. 464p. ISBN 9788576051152
- STEWART, JAMES CÁLCULO Vol.1; trad.7ª ed. SÃO PAULO:Cengage Learning, 2014. 664p. ISBN 9788522112586
- Bibliografia Complementar
- GUIDORIZZI, HAMILTON CÁLCULO Vol.1; 5ª ed. [S.l]:LTC, 2001. 652p. ISBN 9788521612599
- SIMMONS, George Cálculo com geometria analítica: volume 1; 1ª ed. São Paulo:Pearson, 2010. 829p. ISBN 9780074504116
- MEDEIROS, Valéria Zuma Pré-calculo; 2ª ed. São Paulo:Cengage Learning, 2010. 538p. ISBN 9788522107353
ANEXOS