Mudanças entre as edições de "Aula 2 (ELM3605)"
m (ELM3605 - Aula 2 movido para Aula 2 (ELM3605)) |
|||
| (4 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 44: | Linha 44: | ||
z = (-3/2)y + 3 | z = (-3/2)y + 3 | ||
| + | |||
Com isso podemos deifinir o intervalo da primeira integral: | Com isso podemos deifinir o intervalo da primeira integral: | ||
∫(2→0)∫(0→(-3/2)y+3) -2∂y∂z | ∫(2→0)∫(0→(-3/2)y+3) -2∂y∂z | ||
| + | |||
Resolvendo a primeira integral: | Resolvendo a primeira integral: | ||
| Linha 56: | Linha 58: | ||
4 . 3 = '''12''' | 4 . 3 = '''12''' | ||
| + | |||
Cálculo para segunda integral: | Cálculo para segunda integral: | ||
| Linha 64: | Linha 67: | ||
a = -3 | a = -3 | ||
| + | |||
Após estabellecimento do intervalo da integral: | Após estabellecimento do intervalo da integral: | ||
| Linha 72: | Linha 76: | ||
3y = '''0''' | 3y = '''0''' | ||
| + | |||
Cálculo para a terceira integral: | Cálculo para a terceira integral: | ||
| Linha 80: | Linha 85: | ||
a = -2 | a = -2 | ||
| + | |||
Resolvendo a integral: | Resolvendo a integral: | ||
| Linha 86: | Linha 92: | ||
-x |(1→0) . y |(0→-2x+x)= '''-2''' | -x |(1→0) . y |(0→-2x+x)= '''-2''' | ||
| + | |||
| + | |||
| + | E finalizando: | ||
| + | |||
| + | ∫(2→0)∫(0→(-3/2)y+3) -2∂y∂z + ∫(1→0)∫(0→-3x+3) y∂x∂z + ∫(1→0)∫(0→-2x+x) -∂x∂y = | ||
| + | |||
| + | |||
| + | 12 + 0 - 2 = '''''10''''' | ||
| + | |||
| + | Lembrando que esse foi o cálculo de apenas uma superfície... è preciso fazer o Cálculo das outras. | ||
| + | |||
Edição atual tal como às 10h37min de 29 de novembro de 2006
Integral de Campo Vetorial sobre uma Superfície
∫superfície F∂s =
∫superfície (F) . cos(theta)∂s =
∫∫Fx∂y∂z + ∫∫Fy∂x∂z + ∫∫Fz∂x∂y
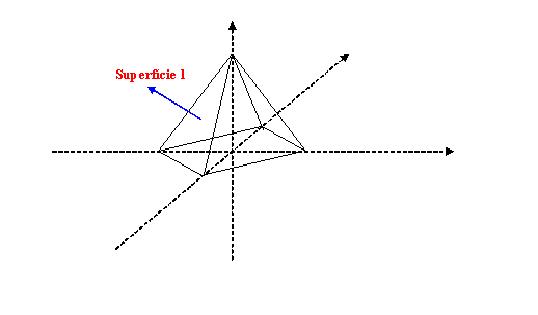
A equação integra o produto escalar a componente normal do campo F a superfície ∂s e o elemento ∂s como na figura anterior.
Simbolos para facilitar .. ƒβεθλΨΩω∞∂ℓ∫≈≠≤≥α→ Página de Ajuda da Wikipedia
Exercício
Determine o fluxo líquido de F = 2 âx + y ây - âz sobre uam superfície delimitada por:
-1 ≤ x ≤ 1
0 ≤ z ≤ 3
-2 ≤ y ≤ 2
Cálculo da superfície 1
z = ay + b
0 = a2 + 3
-3/2 = a
z = (-3/2)y + 3
Com isso podemos deifinir o intervalo da primeira integral:
∫(2→0)∫(0→(-3/2)y+3) -2∂y∂z
Resolvendo a primeira integral:
-2y |(2→0) . z (0→((-3/2)y + 3)
-2(-2) . ((-3/2)y + 3) |(2→0)=
4 . 3 = 12
Cálculo para segunda integral:
z = ax + b
0 = 1a + 3
a = -3
Após estabellecimento do intervalo da integral:
∫(1→0)∫(0→-3x+3) y∂x∂z=
y x |(1→0) z |(0→-3x+3)=
3y = 0
Cálculo para a terceira integral:
y = ax + 2
0 = a + 2
a = -2
Resolvendo a integral:
∫(1→0)∫(0→-2x+x) -∂x∂y=
-x |(1→0) . y |(0→-2x+x)= -2
E finalizando:
∫(2→0)∫(0→(-3/2)y+3) -2∂y∂z + ∫(1→0)∫(0→-3x+3) y∂x∂z + ∫(1→0)∫(0→-2x+x) -∂x∂y =
12 + 0 - 2 = 10
Lembrando que esse foi o cálculo de apenas uma superfície... è preciso fazer o Cálculo das outras.
Simbolos para facilitar .. ƒβεθλΨΩω∞∂ℓ∫≈≠≤≥α→